Appearance
question:Problem 7.2. Denis divided a triangle into nine smaller triangles, as shown in the figure, and placed numbers in them, with the numbers in the white triangles being equal to the sums of the numbers in the adjacent (by sides) gray triangles. After that, Lesha erased the numbers 1, 2, 3, 4, 5, and 6 and wrote the letters A, B, C, D, E, and F in some order. The resulting arrangement of numbers and letters is shown in the figure.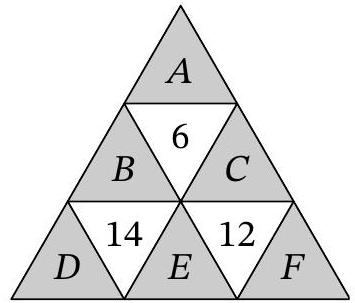Where did the original numbers stand?(a) Instead of the letter A(1) the number 1 stood.(b) Instead of the letter B(2) the number 2 stood.(c) Instead of the letter C(3) the number 3 stood.(d) Instead of the letter D(4) the number 4 stood.(e) Instead of the letter E(5) the number 5 stood.(f) Instead of the letter F(6) the number 6 stood.
answer:Answer: a1 b3 c2 d5 e6 f4.Solution. Note that the number 6 can be uniquely represented as the sum of three numbers from the set of numbers from 1 to 6, which is 6=1+2+3 (or the same numbers in a different order).Now let's look at the numbers B, D, and E. The maximum value of the sum D+E is the sum 5+6=11, and the maximum value of B is 3. According to the condition, the sum of these numbers is exactly 14. Thus, B=3, D and E are 5 and 6 (or vice versa), and A and C are 1 and 2 (or vice versa). By the method of elimination, we get that F=4.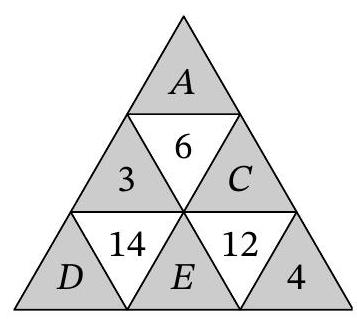The maximum value of the sum C+E is the sum 6+2=8, and according to the condition, 12=C+E+4. From this, we can uniquely restore the entire arrangement of numbers.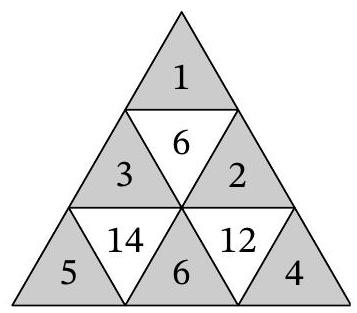
question:3. In a convex quadrilateral A B C D, points E and F are the midpoints of sides B C and C D respectively. Segments A E, A F, and E F divide the quadrilateral into 4 triangles, the areas of which are consecutive natural numbers. What is the maximum possible value of the area of triangle A B D?
answer:3. Let the areas of the triangles be n, n+1, n+2, n+3. Then the area of the quadrilateral A B C D is 4 n+6. It is easy to see that the area of triangle B C D is four times the area of triangle E C F, so this area is at least 4 n. Therefore,S_{A B D}=S_{A B C D}-S_{B C D} leqslant(4 n+6)-4 n=6 .Equality is achieved if triangle E C F has the smallest area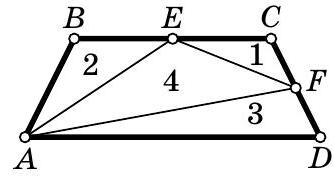Fig. 151 of the four triangles mentioned.It remains to prove that the value 6 is possible. An example is an isosceles trapezoid with bases A D=6, B C=4 and height 2 (the numbers in Fig. 151 denote the areas of the triangles).Comment. It is easy to see that the area of triangle A B D is always either 2 or 6.
question:Given the statement P: forall x in mathbb{R}, x geqslant 2. The correct conclusion for the negation of statement P isA: Statement neg P: forall x in mathbb{R}, x leqslant 2B: Statement neg P: exists {{x}_{0}} in mathbb{R}, x_{0} < 2C: Statement neg P: forall x in mathbb{R}, x leqslant -2D: Statement neg P: exists {{x}_{0}} in mathbb{R}, x_{0} < -2
answer:Analysis:This problem primarily examines the negation of a universal statement resulting in an existential statement, which is a fundamental concept.Step-by-step solution:1. Identify the given statement P: forall x in mathbb{R}, x geqslant 2.2. To negate this statement, we need to find a counterexample that disproves the original statement.3. In other words, we need to find an x_0 in mathbb{R} such that x_0 does not satisfy the condition x geqslant 2.4. The correct negation of the statement P is exists {{x}_{0}} in mathbb{R}, x_{0} < 2.Therefore, the correct answer is boxed{B}.
question:1.049. frac{2^{-2}+5^{0}}{(0.5)^{-2}-5(-2)^{-2}+left(frac{2}{3}right)^{-2}}+4.75.
answer:Solution.begin{aligned}& frac{2^{-2}+5^{0}}{(0.5)^{-2}-5(-2)^{-2}+left(frac{2}{3}right)^{-2}}+4.75=frac{frac{1}{2^{2}}+1}{-frac{1}{(0.5)^{2}}-frac{5}{(-2)^{-2}}+left(frac{3}{2}right)^{2}}+4.75= & =frac{frac{1}{4}+1}{frac{1}{0.25}-frac{5}{4}+frac{9}{4}}+4.75=frac{-frac{4}{4}}{4+1}+4.75=frac{1}{4}+4 frac{3}{4}=5 .end{aligned}Answer: 5.
question:On Lineland there are 2018 bus stations numbered 1 through 2018 from left to right. A self-driving bus that can carry at most N passengers starts from station 1 and drives all the way to station 2018, while making a stop at each bus station. Each passenger that gets on the bus at station i will get off at station j for some j>i (the value of j may vary over different passengers). Call any group of four distinct stations i_1, i_2, j_1, j_2 with i_u< j_v for all u,vin {1,2} a [i]good[/i] group. Suppose that in any good group i_1, i_2, j_1, j_2, there is a passenger who boards at station i_1 and de-boards at station j_1, or there is a passenger who boards at station i_2 and de-boards at station j_2, or both scenarios occur. Compute the minimum possible value of N.[i]Proposed by Yannick Yao[/i]
answer: - We need to find the minimum ( N ) such that every possible good group is covered. - Consider the worst-case scenario where each passenger covers a unique pair ((i, j)). The total number of such pairs is given by the binomial coefficient ( binom{2018}{2} ).4. Calculating the Minimum ( N ): - The number of ways to choose 2 stations out of 2018 is: [ binom{2018}{2} = frac{2018 times 2017}{2} = 2037173 ] - However, we need to ensure that for any four stations ( i_1, i_2, j_1, j_2 ), there is a passenger covering either ( (i_1, j_1) ) or ( (i_2, j_2) ). - This implies that we need to cover all possible pairs ((i, j)) with the minimum number of passengers.5. Finding the Minimum ( N ): - To cover all possible pairs, we need to ensure that each pair is covered by at least one passenger. - The minimum number of passengers required to cover all pairs can be found by considering the maximum number of pairs a single passenger can cover. - Each passenger can cover pairs from their boarding station to any de-boarding station after it.6. Conclusion: - The minimum number of passengers ( N ) required to ensure that every good group is covered is: [ N = 1009 ] - This is because each passenger can cover pairs from their boarding station to any de-boarding station after it, and we need to ensure that all pairs are covered.The final answer is ( boxed{1009} ).
question:1. (40 points) Find the real solutions for the system of equations in w, x, y, z:left{begin{array}{l}w+8 x+3 y+5 z=20 4 w+7 x+2 y+3 z=-20 6 w+3 x+8 y+7 z=20 7 w+2 x+7 y+3 z=-20 .end{array}right.
answer:(1) + (4) gives 8(w+z)+10(x+y)=0.(2) + (3) gives 10(w+z)+10(x+y)=0.Thus, w+z=0 and x+y=0.Substituting y=-x and z=-w into equations (1) and (2) yields 5 x-4 w=20, w+5 x=-20.Eliminating x gives -5 w=40, i.e., w=-8.From this, we get x=-frac{12}{5}, y=frac{12}{5}, z=8.