answer:Let WXYZ be a convex [cyclic quadrilateral](https://artofproblemsolving.com/wiki/index.php/Cyclic_quadrilateral) inscribed in a circle. There are frac{binom{4}{2}}{2} = 3 ways to divide the points into two groups of two.If you pick WX and YZ, you have two sides of the quadrilateral, which do not intersect.If you pick XY and ZW, you have the other two sides of the quadrilateral, which do not intersect.If you pick WY and XZ, you have the diagonals of the quadrilateral, which do intersect.Any four points on the original circle of 1996 can be connected to form such a convex quadrilateral WXYZ, and only placing A and C as one of the diagonals of the figure will form intersecting chords. Thus, the answer is frac{1}{3}, which is option boxed{text{B}}.Notice that 1996 is irrelevant to the solution of the problem; in fact, you may pick points from the entire [circumference](https://artofproblemsolving.com/wiki/index.php/Circumference) of the circle.

answer:1. We start with the given equations: [ 129 - x^2 = xy quad text{and} quad 195 - y^2 = xy ] From these, we can write: [ x^2 + xy = 129 quad text{and} quad y^2 + xy = 195 ]2. Subtract the first equation from the second: [ y^2 + xy - (x^2 + xy) = 195 - 129 ] Simplifying, we get: [ y^2 - x^2 = 66 ] This can be factored using the difference of squares: [ (y - x)(y + x) = 66 ]3. We also know from the equations: [ x^2 + xy = 129 ] and [ y^2 + xy = 195 ] Adding these two equations: [ x^2 + xy + y^2 + xy = 129 + 195 ] Simplifying, we get: [ x^2 + 2xy + y^2 = 324 ] Recognizing the left-hand side as a perfect square: [ (x + y)^2 = 324 ] Taking the square root of both sides: [ x + y = 18 ]4. Now we have two equations: [ (y - x)(y + x) = 66 ] and [ y + x = 18 ] Let ( y - x = a ) and ( y + x = 18 ). Then: [ a cdot 18 = 66 ] Solving for ( a ): [ a = frac{66}{18} = frac{11}{3} ]5. We now have: [ y - x = frac{11}{3} ] and [ y + x = 18 ] Adding these two equations: [ (y - x) + (y + x) = frac{11}{3} + 18 ] Simplifying, we get: [ 2y = frac{11}{3} + frac{54}{3} = frac{65}{3} ] Solving for ( y ): [ y = frac{65}{6} ]6. Subtracting the two equations: [ (y + x) - (y - x) = 18 - frac{11}{3} ] Simplifying, we get: [ 2x = 18 - frac{11}{3} = frac{54}{3} - frac{11}{3} = frac{43}{3} ] Solving for ( x ): [ x = frac{43}{6} ]7. We need to find ( 100m + n ) where ( x = frac{m}{n} ) and ( m ) and ( n ) are relatively prime. Here, ( x = frac{43}{6} ), so ( m = 43 ) and ( n = 6 ).8. Calculating ( 100m + n ): [ 100 cdot 43 + 6 = 4300 + 6 = 4306 ]The final answer is (boxed{4306})

answer:# Answer: 67^{circ}Solution: From the statement cos alpha+cos left(alpha+180^{circ}right)=0, it follows that cos alpha+cos left(alpha+1^{circ}right)+ cdots+cos left(alpha+179^{circ}right)=0. Then cos 2880^{circ}+cos 2881^{circ}+cdots+cos 6479^{circ}=0 and in the exponent only cos 6480^{circ}=1 remains. Similarly, sin alpha+sin left(alpha+1^{circ}right)+cdots+sin left(alpha+179^{circ}right)=0 and sin 2903^{circ}+sin 2904^{circ}+cdots+sin 6502^{circ}=0 cdot sin 6503^{circ}=sin 23^{circ}. Then delta=arccos left(sin 23^{circ}right)=67^{circ}.

answer:SolutionCCicely had her 21st birthday in 1939. Since 1939-21=1918, it follows that she was born in 1918.Now, 1918+100=2018.Therefore Cicely's 100th birthday was in 2018 .

answer:Solution. We have 1992=2^{3} cdot 3 cdot 83, so at least one of the numbers a, b, c, d must be divisible by 83, because otherwise 83 would not appear as a prime factor in their LCM. If two of the numbers are divisible by 83, then their sum would be greater than 100, which is not possible. Therefore, exactly one of the numbers a, b, c, d, e is divisible by 83. Let's set a=83k. k must be one, because otherwise a>100 which is not possible. Therefore, a=83. From b+c+d+e=17 and LCM(83, a, b, c, d, e)=2^{3} cdot 3 cdot 83 it follows that at least one of the numbers b, c, d, e is divisible by 2^{3}=8 because otherwise 2 would appear in the LCM (83, a, b, c, d, e) at a lower power or not at all. If two of the numbers b, c, d, e are divisible by 8, then their sum with a is greater than or equal to 99, so for the remaining two numbers we would have that their sum is 1, which is not possible. Therefore, exactly one of the numbers b, c, d, e is divisible by 8. Let's set b=8m. But m must be one, because otherwise a+b geq 99, i.e., c+d+e leq 1 which is not possible. Therefore, b=8. From c+d+e=9 and LCM(83,8, b, c, d, e)=2^{3} cdot 3 cdot 83, it follows that at least one of the numbers c, d and e must be divisible by 3, because otherwise 3 would not appear as a factor in LCM(83,8, b, c, d, e)=2^{3} cdot 3 cdot 83. Let's set c=3n. If c=3, then d+e=6 and d, e have possible divisors only 1,2,3 and 4; from this, two solutions are obtained: d=e=3 and d=4, e=2. If c=6, then d+e=3 and d, e have possible divisors 1,2,3 and 4, from which the solution d=2, e=1 is obtained. If c geq 9, then d+e leq 0 which is not possible. Therefore, there are three solutions, and they arebegin{aligned}& a=83 ; quad b=8 ; quad c=3 ; quad d=3 ; quad e=3 & a=83 ; quad b=8 ; quad c=3 ; quad d=4 ; quad e=2 & a=83 ; quad b=8 ; quad c=6 ; quad d=2 ; quad e=1end{aligned}

answer:## Solution.Let's prove that the answer is n(n+1).Let a segment denote a length of 1.With each side of the original triangle, there are1+2+cdots+n=frac{n(n+1)}{2}segments.If we color all n(n+1) segments that are parallel to one of the two sides of the original triangle, then there does not exist an equilateral triangle with all three red sides.We still need to prove that we cannot color more than n(n+1) segments without forming an equilateral triangle with three red sides.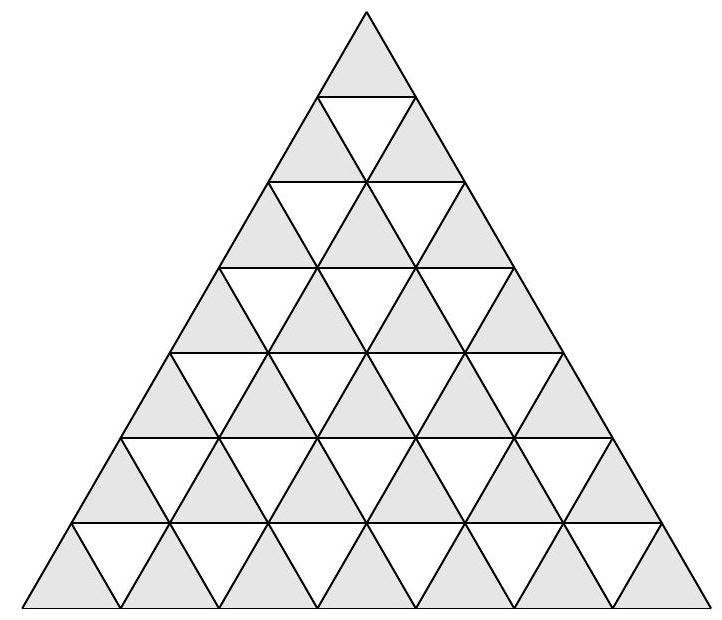Let's shade the triangles whose vertex opposite to the side parallel to the bottom side of the original triangle is pointing upwards, as shown in the figure. The bases of these triangles are segments parallel to the bottom side of the triangle, so there are frac{1}{2} n(n+1) such triangles.No two of these triangles share a side. If more than n(n+1) segments were colored red, then by the Pigeonhole Principle, at least one of the shaded triangles would have all three sides colored red. Therefore, n(n+1) is the maximum number of segments that can be colored red.