Appearance
question:Given vectors overrightarrow{a}=(2,lambda) and overrightarrow{b}=(lambda-1,1), find the value of lambda such that overrightarrow{a} is parallel to overrightarrow{b}.
answer:Since overrightarrow{a} is parallel to overrightarrow{b}, their cross product equals zero, i.e., (λ-1) cdot 2 - 1 cdot λ = 0. Expanding the equation, we get 2λ - 2 - λ = 0, which simplifies to λ^2 - λ - 2 = 0. Factoring the quadratic equation, we obtain (λ - 2)(λ + 1) = 0, which gives us two possible values for λ: λ = -1 or λ = 2.To confirm that these values of λ satisfy the given condition, we can substitute them back into the original vectors to check if they are parallel:1. For λ = -1, we have overrightarrow{a}=(2,-1) and overrightarrow{b}=(-2,1). Since the slope of both vectors is -1/2, they are parallel.2. For λ = 2, we have overrightarrow{a}=(2,2) and overrightarrow{b}=(1,1). Since the slope of both vectors is 1, they are parallel.Thus, both λ = -1 and λ = 2 satisfy the condition, and the final answer is boxed{λ = -1 text{ or } λ = 2}.
question:Given an arithmetic sequence {a_n}, the sum of the first n terms is S_n. If a_2+a_8=15-a_5, then S_9 equals ( ).A: 18B: 36C: 45D: 60
answer:Since a_2+a_8=15-a_5, it follows that a_5=5, thus S_9= frac{9}{2} times 2a_5=45. Therefore, the correct choice is boxed{C}. From the formula of the general term of an arithmetic sequence, we know a_2+a_8=15-a_5 Rightarrow a_5=5. Then, using the formula for the sum of the first n terms of an arithmetic sequence, we find S_9= frac{9}{2} times 2a_5. This problem tests the properties and applications of arithmetic sequences. When solving, it is important to properly use the formula for the general term and the formula for the sum of the first n terms of an arithmetic sequence.
question:In triangle ABC, a, b, c are the sides opposite to angles A, B, C respectively, with A being an acute angle. It is known that vectors overrightarrow {p}=(1, sqrt {3}cos frac {A}{2}), overrightarrow {q}=(2sin frac {A}{2},1-cos2A), and overrightarrow {p}parallel overrightarrow {q}. (1) If a^2-c^2=b^2-mbc, find the value of the real number m. (2) If a= sqrt {3}, find the maximum area of triangle ABC.
answer:Solution: (1) Since overrightarrow {p}parallel overrightarrow {q}, we have 1-2cos2A=2 sqrt {3}sin frac {A}{2}cos frac {A}{2}, which simplifies to 1-cos2A= sqrt {3}sin A, thus 2sin^{2}A= sqrt {3}sin A, and since A is an acute angle, we get sin A= frac { sqrt {3}}{2}, cos A= frac {1}{2}, The equation a^2-c^2=b^2-mbc can be transformed into frac {b^{2}+c^{2}-a^{2}}{2bc}= frac {m}{2} which gives cos A= frac {m}{2}= frac {1}{2}, hence m=1; (2) From (1), we know: cos A= frac {1}{2}, sin A= frac { sqrt {3}}{2}, and since frac {b^{2}+c^{2}-a^{2}}{2bc}= frac {1}{2}, we have bc=b^{2}+c^{2}-a^{2}geq2bc-a^{2}, thus bcleq a^{2}, Therefore, the area of triangle ABC is S_{triangle ABC}= frac {1}{2}bcsin Aleq frac {1}{2}a^{2} frac { sqrt {3}}{2}= frac {3 sqrt {3}}{4}, This maximum area of triangle ABC is boxed{frac {3 sqrt {3}}{4}} when and only when b=c= sqrt {3}.
question:1. The midpoints of adjacent sides of a rectangle with a perimeter of 32 were connected by segments. The same operation was performed on the resulting quadrilateral: the midpoints of adjacent sides were connected by segments (see figure). How many times in total does one need to perform such an operation so that the perimeter of the resulting quadrilateral first becomes less than 1?
answer:Answer: 11.Solution: After two operations, a quadrilateral is obtained, the sides of which are the midlines of triangles with bases parallel to the sides of the original rectangle. Therefore, this quadrilateral is a rectangle, and each of its sides is half the length of the corresponding side of the original rectangle. Thus, after 2 operations, the perimeter is halved. After 5 pairs of operations, the perimeter will decrease by a factor of 2^{5}=32 and will become equal to 1. From the triangle inequality, it is clear that the perimeter decreases with each operation. Therefore, after 11 operations, the perimeter will be less than 1.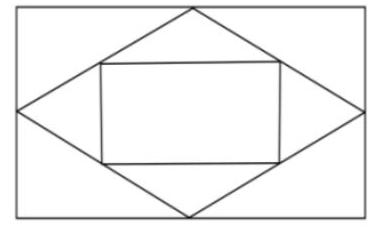Comment: A specific case is considered (for example, calculations are performed for a rectangle with sides given by specific numbers), but the method of calculations can be applied to any rectangle - 4 points; the method is applicable only to rectangles of a certain type - 1-2 points. If the first two operations were not taken into account when counting the number of operations, deduct 1 point. If it is not proven that the perimeter decreases with each operation, deduct 1 point.
question:7. (6 points) There is a dry well, and the depth of the well is measured using a rope. When the rope is folded in half and lowered to the bottom of the well, one end of the rope is 9 m above the well's mouth; when the rope is folded into thirds and lowered to the bottom of the well, one end of the rope is 2 m above the well's mouth. Then the length of the rope is qquad meters, and the depth of the well is qquad meters.
answer:7. (6 points) There is a well without water. To measure the depth of the well, a rope is used. When the rope is folded in half and lowered to the bottom of the well, one end of the rope is 9 m above the well's mouth; when the rope is folded into thirds and lowered to the bottom of the well, one end of the rope is 2 m above the well's mouth. Then the length of the rope is 42 meters, and the depth of the well is underline{12} meters.【Solution】Solution: (9 times 2-2 times 3) div(3-2),begin{array}{l}=(18-6) div 1, =12 div 1, =12 text { (meters), } quad(12+9) times 2, text {, } text { (meters). }end{array}begin{array}{l}=21 times 2, =42 text { (meters). }end{array}Therefore, the answers are: 42,12.
question:II. (16 points) Find all four-digit numbers that satisfy the following conditions: they are divisible by 111, and the quotient obtained is equal to the sum of the digits of the four-digit number.
answer:overline{a b c d}=a times 10^{3}+b times 10^{2}+c times 10+dsatisfies the condition. Thenbegin{array}{l}frac{a times 10^{3}+b times 10^{2}+c times 10+d}{11 i} =9 a+b+frac{a-11 b+10 c+d}{11 i} . because-98 leqslant a-11 b+10 c+d leqslant 108, text { and } overline{a b c d} text { is divisible by }end{array}111,therefore a-11 b+c+d=0 text {, }i.e., 11 b=a+10 c+d.According to the problem, 9 a+b=a+b+c+d,i.e., 8 a=c+d.Substituting into (1) yields11 b=9(a+c) text {. }And from c+d leqslant 18, we know a=1 or 2.Thus, from equation (2) we getb=9, a=2, c=9 text {. }Then, from 8 a=c+d, we get d=7.Therefore, the required four-digit number is 2997.