Appearance
question:Given the function f(x)=ax^{3}+ sqrt {b}x^{2}-a^{2}x (a > 0), there exist real numbers x_{1} and x_{2} satisfying the following conditions: (1) x_{1} < x_{2}; (2) f′(x_{1})=f′(x_{2})=0; (3) |x_{1}|+|x_{2}|=2. (1) Prove that: 0 < aleqslant 3; (2) Find the range of values for b.
answer:Solution: (1) Since the function f(x)=ax^{3}+ sqrt {b}x^{2}-a^{2}x, we have f′(x)=3ax^{2}+2 sqrt {b}x-a^{2}. Given that x_{1} 0, we get x_{1} < 0 < x_{2}. Since |x_{1}|+|x_{2}|=2, we have x_{2}-x_{1}=2. Thus, x_{1} and x_{2} are the two real roots of the equation t^{2}-2t+ frac {a}{3}=0. Since the equation has solutions, we have triangle =4- frac {4a}{3}geqslant 0, which gives 0 < aleqslant 3. Therefore, the range of a is (0,3].(2) From b=3a^{2}(3-a)=-3a^{3}+9a^{2}, we have b′=-9a^{2}+18a. Setting b′=0, we find a=0 or a=2, thus, for 0 < aleqslant 2, b′geqslant 0, meaning b is monotonically increasing on (0,2]. Therefore, we have 0leqslant bleqslant 12.Therefore, the answers are: (1) The range of a is boxed{(0,3]}. (2) The range of b is boxed{[0,12]}.
question:Let f: [0,1]rightarrow(0,+infty) be a continuous function.
a) Show that for any integer ngeq 1, there is a unique division 0=a_{0}<a_{1}<ldots<a_{n}=1 such that int_{a_{k}}^{a_{k+1}}f(x), dx=frac{1}{n}int_{0}^{1}f(x), dx holds for all k=0,1,ldots,n-1.
b) For each n, consider the a_{i} above (that depend on n) and define b_{n}=frac{a_{1}+a_{2}+ldots+a_{n}}{n}. Show that the sequence (b_{n}) is convergent and compute it's limit.
answer: Part (a)1. Define the cumulative distribution function: Let (Phi(t) = int_{0}^{t} f(x) , dx). Since (f(x)) is continuous and positive on ([0,1]), (Phi(t)) is strictly increasing and continuous on ([0,1]).2. Determine the total integral: Let (I = int_{0}^{1} f(x) , dx). Since (f(x)) is positive and continuous, (I > 0).3. Divide the interval ([0,1]) into (n) parts: We need to find points (0 = a_0 < a_1 < ldots < a_n = 1) such that: [ int_{a_k}^{a_{k+1}} f(x) , dx = frac{I}{n} quad text{for all } k = 0, 1, ldots, n-1. ]4. Use the inverse function: Since (Phi(t)) is strictly increasing and continuous, it has a well-defined inverse function (Phi^{-1}). Define: [ a_i = Phi^{-1}left(frac{iI}{n}right) quad text{for } i = 0, 1, ldots, n. ]5. Verify the integral condition: For each (k): [ int_{a_k}^{a_{k+1}} f(x) , dx = Phi(a_{k+1}) - Phi(a_k) = frac{(k+1)I}{n} - frac{kI}{n} = frac{I}{n}. ] This shows that the division (0 = a_0 < a_1 < ldots < a_n = 1) satisfies the required condition. Part (b)1. Define the sequence (b_n): For each (n), let: [ b_n = frac{a_1 + a_2 + ldots + a_n}{n}. ]2. Express (b_n) in terms of (Phi^{-1}): Using the definition of (a_i): [ b_n = frac{1}{n} sum_{i=1}^{n} Phi^{-1}left(frac{iI}{n}right). ]3. Consider the limit of (b_n): As (n to infty), the sum (frac{1}{n} sum_{i=1}^{n} Phi^{-1}left(frac{iI}{n}right)) approximates the integral: [ lim_{n to infty} b_n = frac{1}{I} int_{0}^{I} Phi^{-1}(t) , dt. ]4. Change of variables: Let (u = Phi(x)), then (du = f(x) , dx) and the limits change from (0) to (1) for (x) and from (0) to (I) for (u). Thus: [ int_{0}^{I} Phi^{-1}(t) , dt = int_{0}^{1} x f(x) , dx. ]5. Compute the limit: Therefore: [ lim_{n to infty} b_n = frac{1}{I} int_{0}^{1} x f(x) , dx. ]The final answer is ( boxed{ frac{int_{0}^{1} x f(x) , dx}{int_{0}^{1} f(x) , dx} } ).
question:5. If the sequence left{a_{n}right}: a_{1}, a_{2}, cdots, a_{5} satisfies0 leqslant a_{1}<a_{2}<a_{3}<a_{4}<a_{5},and for any i, j(1 leqslant i leqslant j leqslant 5), a_{j}-a_{i} is in the sequence.(1) a_{1}=0;(2) a_{5}=4 a_{2};(3) left{a_{n}right} is an arithmetic sequence;(4) The set A=left{a_{i}+a_{j} mid 1 leqslant i leqslant j leqslant 5right} contains nine elements.The number of correct statements is ( ).(A) 1(B) 2(C) 3(D) 4
answer:5. D.Since a_{1}-a_{1}=0 in left{a_{n}right}, we have a_{1}=0. Therefore, statement (1) is correct.Since 0=a_{1}<a_{3}-a_{2}<a_{4}-a_{2}<a_{5}-a_{2}<a_{5}, and a_{3}-a_{2}, a_{4}-a_{2}, a_{5}-a_{2} in left{a_{n}right}, we havebegin{array}{l}a_{3}-a_{2}=a_{2}, a_{4}-a_{2}=a_{3}, a_{5}-a_{2}=a_{4} Rightarrow a_{2}-a_{1}=a_{3}-a_{2}=a_{4}-a_{3}=a_{5}-a_{4}.end{array}Thus, left{a_{n}right} is an arithmetic sequence, and left{a_{n}right} is0, d, 2d, 3d, 4d.Therefore, a_{5}=4a_{2}.Hence, statements (2) and (3) are correct.The set A=left{a_{i}+a_{j} mid 1 leqslant i leqslant j leqslant 5right} contains nine elements.
question:In triangle ABC, the lengths of the sides opposite to angles A, B, C are a, b, c respectively, and 2cos A(acos B+bcos A)=c.(I) Find the measure of angle A;(II) If the area of triangle ABC is S=10sqrt{3}, and a=7, find the perimeter of triangle ABC.
answer:(I) By the Sine Law: frac{a}{sin A}=frac{b}{sin B}=frac{c}{sin C}=2R,we have a=2Rsin A, b=2Rsin B, c=2Rsin C.Then from the given information, we get: 2cos A(sin Acos B+sin Bcos A)=sin C, (1)therefore 2cos Asin(A+B)=sin C, (2)therefore 2cos Asin C=sin C, (3)Since 0<C<pi, we have sin Cneq 0,therefore cos A=frac{1}{2}, Solving for A gives A=frac{pi}{3}, (4)(II) From (I), we know A=frac{pi}{3}, and a=7By the Cosine Law: b^2+c^2-bc=49, (ast) (6)Since the area of triangle ABC is S=frac{1}{2}bcsin A=10sqrt{3}, we have bc=40, (astast) (7)From (ast) and (astast), we get: b^2+c^2-bc=(b+c)^2-3bc=49, (8)Solving for b+c gives b+c=13, (9)therefore The perimeter of triangle ABC is a+b+c=boxed{20}. (10)
question:1. Brothers Anže and Uroš have a total of 312 euros. If Anže gave Uroš 4 % of his amount, Uroš would have 4 times as much as Anže. Calculate the amounts that Anže and Uroš have.
answer:1. We consider that the brothers together have x+y=312 euros. From the problem statement, we write the equation left(x-frac{4}{100} xright) cdot 4=y+frac{4}{100} x. In the equation, we remove the parentheses 4 x-frac{4}{25} x=312-x+frac{1}{25} and rearrange it 96 x+24 x=7800. We calculate x=65. Then we calculate y=247. We write the answer: Anže had 65 euros, and Uroš had 247 euros.We write the relationship x+y=312 or x=312-y ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots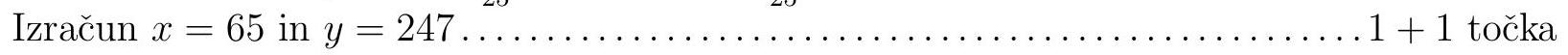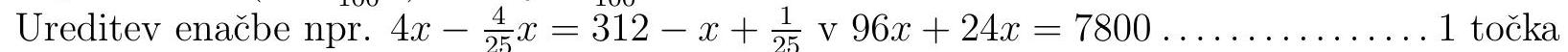Answer . .........................................................................................................
question:Given vectors overrightarrow{m}=(cos alpha ,-1) and overrightarrow{n}=(2,sin alpha ), where alpha in left( 0,frac{pi }{2} right), and overrightarrow{m}bot overrightarrow{n}.(1) Find the value of cos 2alpha;(2) If sin (alpha -beta )=frac{sqrt{10}}{10}, and beta in left( 0,frac{pi }{2} right), find the angle beta.
answer:Solution:(1) Since overrightarrow{m}bot overrightarrow{n},therefore overrightarrow{m}cdot overrightarrow{n}=0,therefore 2cos alpha =sin alpha,Since {sin }^{2}alpha+{cos }^{2}alpha=1, and alphainleft(0, frac{pi}{2}right),therefore cos alpha= frac{ sqrt{5}}{5},sin alpha= frac{2 sqrt{5}}{5},therefore cos 2alpha=2{cos }^{2}alpha-1=- frac{3}{5};(2) Since 0 < beta < frac{pi}{2},therefore - frac{pi}{2} < alpha-beta < frac{pi}{2},Since sin left(alpha-betaright)= frac{ sqrt{10}}{10},therefore cos left(alpha-betaright)= frac{3 sqrt{10}}{10},Since sin beta=sin left[alpha-left(alpha-betaright)right],=sin alphacos left(alpha-betaright)-cos alphasin left(alpha-betaright),= frac{2 sqrt{5}}{5}times frac{3 sqrt{10}}{10}- frac{ sqrt{5}}{5}times frac{ sqrt{10}}{10},= frac{ sqrt{2}}{2},Since 0 < beta < frac{pi}{2},therefore beta= frac{pi}{4}.Thus, the answers are boxed{-frac{3}{5}} for part (1) and boxed{frac{pi}{4}} for part (2).