answer:Let's solve the problem more generally for n teams, where n is an odd number. We will represent each team with a point. After a match between two teams, an arrow should point from the losing team to the winning team. (In this context, we can assume that there has never been a tie.)If the teams A, B, and C have beaten each other in a cycle, which can happen in two ways, then the triangle ABC is called directed. Otherwise, the triangle is not directed.Provide an estimate for the number of non-directed triangles.In every non-directed triangle, there is exactly one vertex such that the team represented by this vertex has beaten the other two. We will count the non-directed triangles according to the "winning" vertex.Let the teams be represented by the points A_{1}, A_{2}, ldots, A_{n}, and let d_{i} denote the number of wins for A_{i}. Since there were a total of binom{n}{2} matches, sum_{i=1}^{n} d_{i}=frac{n(n-1)}{2}. Then, binom{d_{i}}{2} non-directed triangles are associated with the vertex A_{i}, since we need to choose two from the teams it has beaten.Thus, the total number of non-directed triangles is: sum_{i=1}^{n}binom{d_{i}}{2}.By the inequality between the arithmetic mean and the quadratic mean:begin{gathered}sum_{i=1}^{n}binom{d_{i}}{2}=frac{1}{2} sum_{i=1}^{n} d_{i}^{2}-frac{1}{2} sum_{i=1}^{n} d_{i}=frac{1}{2} n frac{sum_{i=1}^{n} d_{i}^{2}}{n}-frac{1}{2} sum_{i=1}^{n} d_{i} geq frac{1}{2} nleft(frac{sum_{i=1}^{n} d_{i}}{n}right)^{2}-frac{1}{2} sum_{i=1}^{n} d_{i}= =frac{1}{2} nleft(frac{n-1}{2}right)^{2}-frac{1}{2} frac{n(n-1)}{2}=frac{n^{3}-4 n^{2}+3 n}{8}end{gathered}Can equality hold here? Yes, if we can provide a directed complete graph for whichd_{1}=d_{2}=cdots=d_{n}=frac{n-1}{2}Let n=2 k+1. Then one possible construction is as follows:If 1 leq i<j leq 2 k+1 and j-i is greater than k, then A_{j} beat A_{i}, otherwise A_{i} beat A_{j}. It is easy to verify that in this case,d_{1}=d_{2}=cdots=d_{n}=frac{n-1}{2}Since there are binom{n}{3} triangles in total, the number of directed triangles in our case isbinom{n}{3}-frac{n^{3}-4 n^{2}+3 n}{8}=frac{n(n-1)(n-2)}{6}-frac{n^{3}-4 n^{2}+3 n}{8}=frac{n^{3}-n}{24}For the case n=23, this is 506, so at most 506 cycles of wins could have occurred during the tournament.Based on the work of András Juhász (Fazekas M. Főv. Gyak. Gimn., 10th grade)

answer:From the given condition, we have f(7) = 6.Therefore, f(f(7)) = f(6) = 2,Therefore, f(f(f(7))) = f(2) = 4,Therefore, f(f(f(f(7)))) = f(4) = 5,Therefore, f(f(f(f(f(7))))) = f(5) = 9,Therefore, f(f(f(f(f(7))))) = f(f(9)) = 5,Therefore, f(f(f(f(f(f(7)))))) = f(5) = 3,Therefore, f(f(f(f(f(f(f(7))))))) = f(3) = 1,After this, a cycle occurs, and every function value equals zero,Thus, it is derived that f{fldots f[f(7)]} (with a total of 2007 f's) = 1.Hence, the answer is boxed{1}.

answer:Continue M N until it intersects one of the lateral sides of the trapezoid.## SolutionDraw a line through point M parallel to the bases. Let K and N_{1} be the points of intersection of this line with side C D and diagonal B D, respectively (see figure). From Thales' theorem, it follows that D K: K C = A M: M C = 1: 4, D N_{1}: N_{1} B = D K: K C = 1: 4. Therefore, point N_{1} coincides with point N. Consequently, M N | A D.From the similarity of triangles C K M and C D A, we find that M K = 4 / 5 A D = 4 / 5 a, and from the similarity of triangles D K N and D C B, we find that K N = 1 / 5 B C = 1 / 5 b.Therefore, M N = M K - K N = 1 / 5 (4 a - b).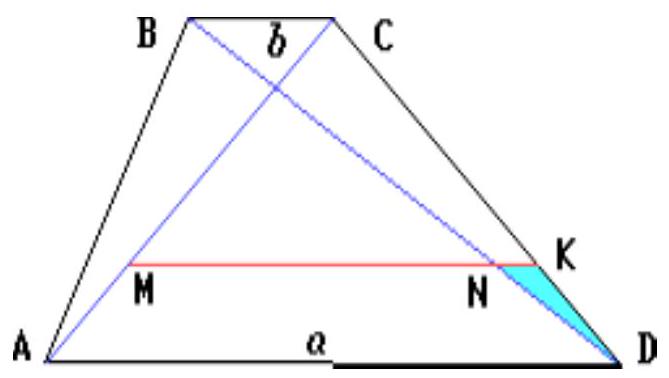Answer1 / 5 (4 a - b).Send a comment

answer:The points A, D, S lie in a plane varepsilon^{prime}, which is perpendicular to the plane varepsilon through A, B, C and D; for by assumption, A D perp A B and, if S neq A, also S A perp A B.In the case S=A, let varepsilon^{prime} be the plane perpendicular to varepsilon through A and D. Therefore, in any case, C D perp varepsilon^{prime} and thus |angle C D S|=90^{circ}.

answer:We draw a diagram to make our work easier:Assume that AB is of length 1. Therefore, the area of ABCDEF is frac{3sqrt 3}2. To find the area of WCXYFZ, we draw overline{CF}, and find the area of the trapezoids WCFZ and CXYF. From this, we know that CF=2. We also know that the combined heights of the trapezoids is frac{sqrt 3}3, since overline{ZW} and overline{YX} are equally spaced, and the height of each of the trapezoids is frac{sqrt 3}6. From this, we know overline{ZW} and overline{YX} are each frac 13 of the way from overline{CF} to overline{DE} and overline{AB}, respectively. We know that these are both equal to frac 53.We find the area of each of the trapezoids, which both happen to be frac{11}6 cdot frac{sqrt 3}6=frac{11sqrt 3}{36}, and the combined area is frac{11sqrt 3}{18}.We find that dfrac{frac{11sqrt 3}{18}}{frac{3sqrt 3}2} is equal to frac{22}{54}=boxed{textbf{(C)} frac{11}{27}}.

answer:【Analysis】300 square centimetersConnecting lines as shown in the figure can divide the shape into 6 equal parts, where the area of any one part is 10 times 10 div 2=50 square centimeters; therefore, the area of pentagon A B E F D is 50 times 6=300 square centimeters.