answer:begin{array}{l}text {-1.A. } x=2^{n+1}+2^{n}=2^{2}left(2^{n-1}+2^{n-2}right)=4 y .end{array}The translation is as follows:begin{array}{l}text {-1.A. } x=2^{n+1}+2^{n}=2^{2}left(2^{n-1}+2^{n-2}right)=4 y .end{array}Note: The original text is already in a mathematical form that is the same in both Chinese and English, so the translation is identical to the original.

answer:(1) f'(x)=ln x+1,therefore f'(e)=2, given f(e)=e,therefore The equation of the tangent line to the function f(x) at x=e is y-e=2(x-e),i.e., boxed{2x-y-e=0};(2) If there exists an x_{0}in[1,e] such that f(x_{0}) frac {2ln x_{0}}{x_{0}}.Let h(x)= frac {2ln x}{x},when xin[1,e), h'(x)= frac {2(1-ln x)}{x^{2}} > 0 always holds.Therefore, h(x)= frac {2ln x}{x} is monotonically increasing on [1,e],when x=1, h(x)_{min}=0,therefore the range of values for the real number a is boxed{(0,+infty)};(3) From the problem, we have: xln x > (k-3)x-k+2 always holds when x > 1,i.e., k 0 always holds when x > 1,therefore m(x) is monotonically increasing on (1,+infty), and m(3)=1- ln 3 0,therefore there exists a unique real number b(bin(3,4)) in (1,+infty) such that m(x)=0, i.e., m(b)=0,when 1 b, m(x) > 0, i.e., F'(x) > 0,therefore F(x) is monotonically decreasing on (1,b) and monotonically increasing on (b,+infty),therefore F(x)_{min}=F(b)= frac {bln b+3b-2}{b-1}= frac {b(b-2)+3b-2}{b-1}=b+2in(5,6),therefore k < b+2, and kin Z,therefore the maximum value of the integer k is boxed{5}.

answer:First, we simplify the complex number frac{1+i}{1-i} + frac{1}{2}b by multiplying the numerator and the denominator of the first fraction by the conjugate of the denominator:frac{1+i}{1-i} + frac{1}{2}b = frac{(1+i)(1+i)}{(1-i)(1+i)} + frac{1}{2}b = frac{2i}{2} + frac{1}{2}b = i + frac{1}{2}bSince the real part and the imaginary part of the complex number frac{1+i}{1-i} + frac{1}{2}b are equal, we have:frac{1}{2}b = 1Solving for b, we get:b = 2Therefore, the value of b is boxed{2}.

answer:(1) For a=1, we have f(x) = |x-1| + |2x-1|,To solve f(x) leqslant 2, we get |x-1| + |2x-1| leqslant 2.This inequality can be rewritten using cases as follows:- For x leqslant frac{1}{2}, the inequality becomes 1-x+1-2x leqslant 2.- For frac{1}{2} < x < 1, the inequality becomes 1-x+2x-1 leqslant 2.- For x geqslant 1, the inequality becomes x-1+2x-1 leqslant 2.Solving these, we get x in [0, frac{1}{2}], x in (frac{1}{2}, 1), and x in [1, frac{4}{3}] respectively.Therefore, the solution set of the original inequality is x in left[0, frac{4}{3}right].boxed{x in left[0, frac{4}{3}right]}(2) Since the solution set of f(x) leqslant |2x+1| includes left[frac{1}{2}, 1right],It follows that the inequality f(x) leqslant |2x+1| holds for all x in left[frac{1}{2}, 1right],Which translates to |x-a| + |2x-1| leqslant |2x+1| for all x in left[frac{1}{2}, 1right].Simplifying this condition gives |x-a| + 2x - 1 leqslant 2x + 1 for x in left[frac{1}{2}, 1right],Implying |x-a| leqslant 2 for all x in left[frac{1}{2}, 1right],This means x-2 leqslant a leqslant x+2 holds for all x in left[frac{1}{2}, 1right].Therefore, we can establish the bounds for a by finding the maximum of (x-2) and the minimum of (x+2) within the interval left[frac{1}{2}, 1right],Concluding -1 leqslant a leqslant frac{5}{2},Hence, the range of values for a is left[-1, frac{5}{2}right].boxed{a in left[-1, frac{5}{2}right]}

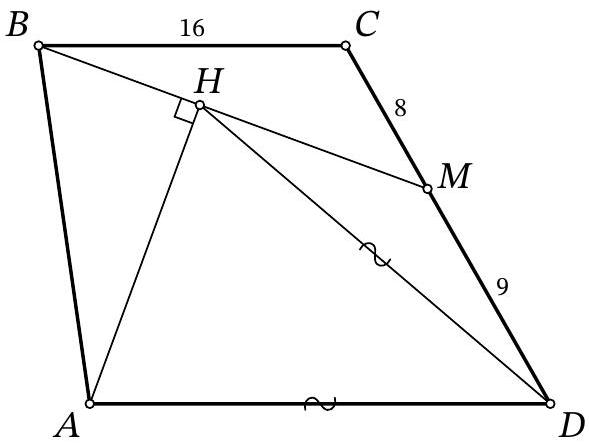
answer:Answer: 18.Solution. Let the lines B M and A D intersect at point K (Fig. 5). Since B C | A D, triangles B C M and K D M are similar by angles, from which we obtain D K = B C cdot frac{D M}{C M} = 16 cdot frac{9}{8} = 18.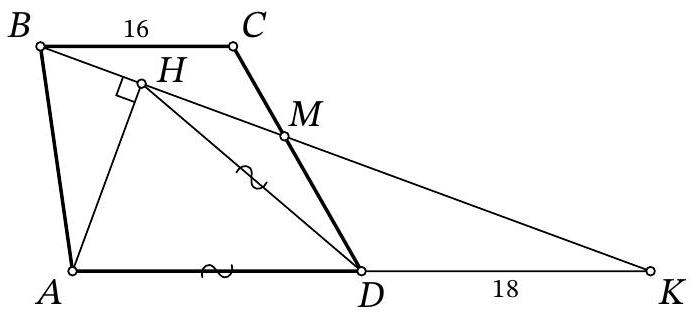Fig. 5: to the solution of problem 9.8In the isosceles triangle A D H, draw the height and median D S. Then, in triangle A H K, the segment D S passes through the midpoint of side A H and is parallel to H K. Therefore, D S is the midline of this triangle, and A D = D K = 18.Remark. If in a right triangle a point on the hypotenuse is equidistant from two vertices of the triangle, then it is equidistant from all three vertices of the triangle.## 10th Grade

answer:Solution: Construct the identityfrac{a}{a+b+c}+frac{b}{a+b+c}+frac{c}{a+b+c}=1 text {. }Subtract the above identity from the given equation to getbegin{array}{l}left(frac{a}{b+c}-frac{a}{a+b+c}right)+left(frac{b}{a+c}-frac{b}{a+b+c}right)+ left(frac{c}{a+b}-frac{c}{a+b+c}right)=0 .end{array}Simplifying, we getbegin{array}{l}frac{a^{2}}{(b+c)(a+b+c)}+frac{b^{2}}{(a+c)(a+b+c)}+ frac{c^{2}}{(a+b)(a+c+b)}=0,end{array}which means squarebegin{array}{l}frac{1}{a+b+c}left(frac{a^{2}}{b+c}+frac{b^{2}}{a+c}+frac{c^{2}}{a+b}right)=0 . text { Hence } frac{a^{2}}{b+c}+frac{b^{2}}{a+c}+frac{c^{2}}{a+b}=0 .end{array}