Appearance
question:The figure shows a regular dodecagon decomposed into six equilateral triangles, six squares, and one regular hexagon, all with the same side length.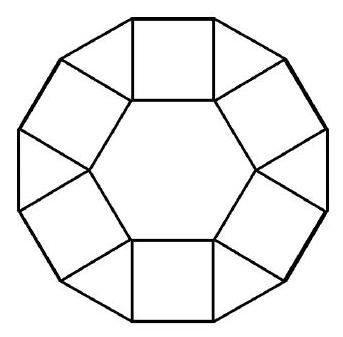a) If each triangle has an area of 1 mathrm{~cm}^{2}, what is the area of the hexagon?b) The figure below was obtained by removing twelve equilateral triangles from a regular dodecagon whose side measures 1 mathrm{~cm}. What is the area of this figure?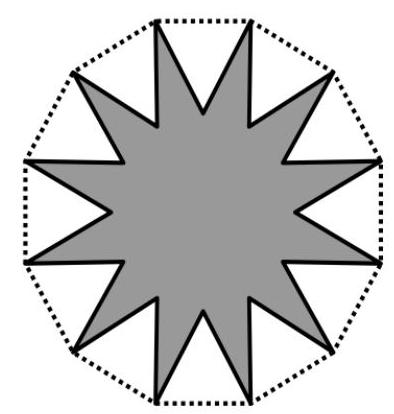c) The figure below was obtained by removing two regular hexagons from a regular dodecagon whose side measures 1 mathrm{~cm}. What is the area of this figure?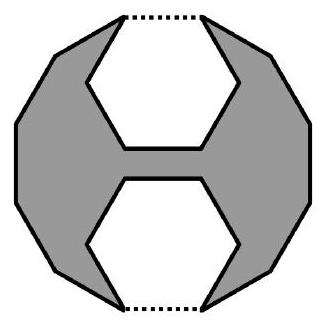
answer:Solutiona) The figure below shows that the hexagon can be decomposed into six triangles equal to the triangles that make up the dodecagon. Since each of these triangles has an area of 1 mathrm{~cm}^{2}, it follows that the hexagon has an area of 6 mathrm{~cm}^{2}.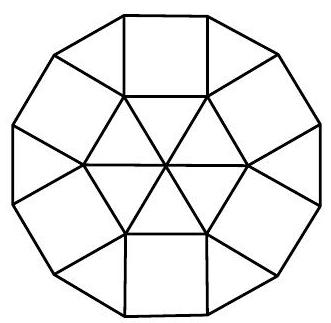b) 1^{st} solution: The figure from the previous item shows that the dodecagon can be decomposed into twelve equal equilateral triangles and six squares. Thus, by removing twelve triangles from the dodecagon, the star that remains has an area equal to the area of six squares. Since the side of the dodecagon measures 1 mathrm{~cm}, each square has an area of 1 mathrm{~cm}^{2}, and thus the area of the star is 6 mathrm{~cm}^{2}.2^{nd} solution: We can decompose the central hexagon of the star into six triangles and "fit" them as indicated in the figure below. The figure thus obtained has the same area as the star and consists of six squares with a side of 1 mathrm{~cm}; its area is then 6 mathrm{~cm}^{2}.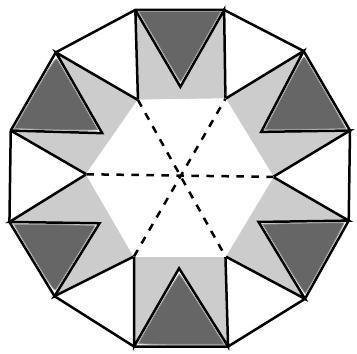c) The figure below shows that the two hexagons removed have the same area as twelve equilateral triangles; as in item b), the gray region has the same area as six squares with a side of 1 mathrm{~cm}; its area is then 6 mathrm{~cm}^{2}.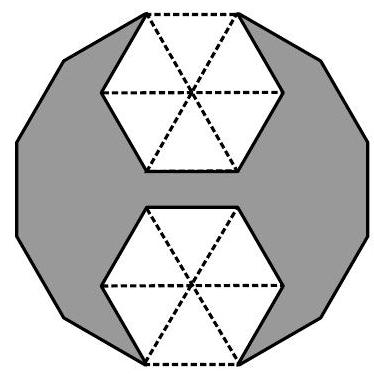
question:A natural number n was alternately divided by 29, 41 and 59. The result was three nonzero remainders, the sum of which equals n. Find all such n
answer:1. Let ( n equiv a pmod{29} ), ( n equiv b pmod{41} ), and ( n equiv c pmod{59} ). We are given that ( a + b + c = n ).2. Since ( a, b, c ) are remainders, we have ( 0 < a < 29 ), ( 0 < b < 41 ), and ( 0 < c < 59 ). Therefore, ( n = a + b + c leq 28 + 40 + 58 = 126 ).3. We also know that ( n > 59 ) because ( c ) is a remainder when ( n ) is divided by 59, and ( c ) must be nonzero.4. Thus, ( 60 leq n leq 126 ).5. We need to find ( n ) such that ( n = a + b + c ) and ( n equiv a pmod{29} ), ( n equiv b pmod{41} ), ( n equiv c pmod{59} ).6. From ( n = a + b + c equiv c pmod{59} ), we get ( a + b equiv 0 pmod{59} ). Therefore, ( a + b = 59 ).7. From ( n = a + b + c equiv b pmod{41} ), we get ( a + c equiv 0 pmod{41} ). Therefore, ( a + c = 41 ) or ( a + c = 82 ).8. Case 1: ( a + c = 41 ) and ( a + b = 59 ). - Then ( n = a + b + c = a + 59 - a + 41 - a = 100 - a ). - We need ( 100 - a equiv a pmod{29} ). - This simplifies to ( 100 equiv 2a pmod{29} ). - Solving ( 2a equiv 13 pmod{29} ), we get ( a = 21 ). - Then ( c = 41 - a = 20 ) and ( b = 59 - a = 38 ). - Therefore, ( n = 21 + 38 + 20 = 79 ).9. Case 2: ( a + c = 82 ) and ( a + b = 59 ). - Then ( n = a + b + c = a + 59 - a + 82 - a = 141 - a ). - We need ( 141 - a equiv a pmod{29} ). - This simplifies to ( 141 equiv 2a pmod{29} ). - Solving ( 2a equiv 24 pmod{29} ), we get ( a = 27 ). - Then ( c = 82 - a = 55 ) and ( b = 59 - a = 32 ). - Therefore, ( n = 27 + 32 + 55 = 114 ).10. We have found two possible values for ( n ): ( 79 ) and ( 114 ).The final answer is ( boxed{79 text{ and } 114} ).
question:If the complex number z= frac{4+3i}{2-i}, then the imaginary part of the complex number z is _______, and the modulus of overline{z}cdot(2-i) is _______.
answer:To find the imaginary part of the complex number z and the modulus of overline{z}cdot(2-i), we proceed as follows:First, simplify the expression for z:begin{align*}z &= frac{4+3i}{2-i} &= frac{(4+3i)(2+i)}{(2-i)(2+i)} &= frac{8+4i+6i+3i^2}{4+2i-2i-i^2} &= frac{8+4i+6i-3}{4+1} &= frac{5+10i}{5} &= 1+2i,end{align*}So the imaginary part of z is 2.For the second part, find the modulus of overline{z}cdot(2-i):begin{align*}overline{z} &= overline{1+2i} = 1 - 2i, overline{z}cdot(2-i) &= (1 - 2i)(2-i) &= 2 - i - 4i + 2i^2 &= 2 - 5i - 2 &= -5i.end{align*}Therefore, the modulus of overline{z}cdot(2-i) is |{-5i}| = 5.Thus, the imaginary part of z is boxed{2}, and the modulus of overline{z}cdot(2-i) is boxed{5}.
question:114 The sides of a right triangle are all positive integers. One of the legs is 1575 less than the hypotenuse, and the other leg is less than 1991. Then the length of the hypotenuse of this right triangle is qquad .
answer:1141799 . Let the hypotenuse of a right-angled triangle be c, and the two legs be a and b. Thenbegin{aligned}a^{2} & =c^{2}-b^{2}=(c-b)(c+b) & =1575 times(c+b) & =3^{2} times 5^{2} times 7 times(c+b),end{aligned}Thus, 105 mid a. Also, a^{2}=1575(c+b)>1575 a, so1575<a<1991 .Therefore,105 times 15<a<105 times 19 .Since c-b is odd, c+b is also odd, hence a is odd,a=105 times 17=1785 .Furthermore, c=1799.
question:10. Given vectors vec{a}, vec{b}, vec{c}, vec{d}, and at least one of vec{a}, vec{b} is not a zero vector, the function of real number t is f(t)=|t vec{a}+vec{c}|^{2}+|t vec{b}+vec{d}|^{2}, then when t= qquad, f(t) reaches its minimum value.
answer:10. begin{array}{l}-frac{vec{a} cdot vec{c}+vec{b} cdot vec{d}}{|vec{a}|^{2}+|vec{b}|^{2}} f(t)=t^{2} vec{a}^{2}+2(vec{a} cdot vec{c}) t+vec{c}^{2}+t^{2} vec{b}^{2}+2(vec{b} cdot vec{d}) t+vec{d}^{2} =left(vec{a}^{2}+vec{b}^{2}right) t^{2}+2(vec{a} cdot vec{c}+vec{b} cdot vec{d}) t+vec{c}^{2}+vec{d}^{2} .end{array}
question:1. Among the positive integers not greater than 2017, there are qquad numbers that are divisible by 12 but not by 20.
answer:left[frac{2017}{12}right]-left[frac{2017}{60}right]=168-33=135 .Solveleft[frac{2017}{12}right]-left[frac{2017}{60}right]=168-33=135 .