answer:118. It is clear that the second square can be placed so that its vertices fall on the points of tangency of the circle with the sides of the first square (see Fig. 18). After this, it is not difficult to verify that the desired ratio of the areas of the squares is 2.Fig. quad 18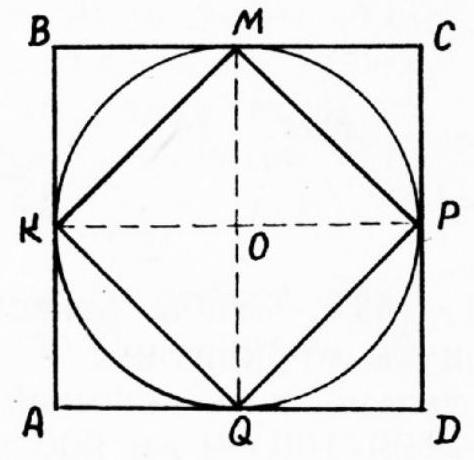24

answer:Since the function f(x) = 2^{-x} and the function g(x) = log_{frac{1}{2}}x are inverse functions of each other, the graphs of the two functions are symmetric about the line y=x. Therefore, the correct answer is: boxed{C}. By utilizing the symmetry of inverse functions about the line y=x, the result can be deduced. This question examines the relationship between functions and inverse functions, testing basic knowledge.

answer:2. Let x_{i}=lambda+y_{i} (where lambda is a parameter to be determined). Thenbegin{array}{l}sum_{i=1}^{n} a_{i} x_{i}^{2}=sum_{i=1}^{n} a_{i}left(lambda+y_{i}right)^{2} =lambda^{2} q+2 lambda sum_{i=1}^{n} a_{i} y_{i}+sum_{i=1}^{n} a_{i} y_{i}^{2} . text { and } sum_{i=1}^{n} a_{i} x_{i}=sum_{i=1}^{n} a_{i}left(lambda+y_{i}right) =lambda q+sum_{i=1}^{n} a_{i} y_{i}=p,end{array}Thus, taking lambda=frac{p}{q}, we have sum_{i=1}^{n} a_{i} y_{i}=0.Substituting into equation (1) givessum_{i=1}^{n} a_{i} x_{i}^{2}=frac{p^{2}}{q}+sum_{i=1}^{n} a_{i} y_{i}^{2} geqslant frac{p^{2}}{q},with equality holding if and only if y_{1}=y_{2}=cdots=y_{n}=0, i.e., x_{1}=x_{2}=cdots=x_{n}=lambda=frac{p}{q}.Therefore, sum_{i=1}^{n} a_{i} x_{i}^{2} attains its minimum value frac{p^{2}}{q}.

answer:Let X_{n} denote the random variable "Number of visible people among n people". What happens when the n-th person is added to the end of the queue?With probability 1 / n, he is taller than all the others, and with probability { }^{n-1 / n}, he is not the tallest. In the first case, one more person will be visible, and in the second case, the number of visible people will not change. Therefore, X_{n}=1 /{ }_{n}left(X_{n-1}+1right)+{ }^{n-} 1 / X_{n-1} cdotLet's move to expectations: mathrm{E} X_{n}=mathrm{E} X_{n-1}+1 / n=mathrm{E} X_{n-2}+1 / n-1+1 / n=ldots=mathrm{E} X_{1}+1 / 2+1 / 3+ldots+1 / n. mathrm{E} X_{1}=1, since one person is always visible. Therefore, mathrm{E} X_{n}=1+1 / 2+1 / 3+ldots+1 / n.## Answer1+1 / 2+1 / 3+ldots+1 / n

answer:4. The faster ant is ahead of the slower one and is moving away from it.It is clear that situation 1 can over time turn into situation 2, and situation 3 can turn into situation 4. But if the ants at some point find themselves in situation 2 or 4, then from that moment on, they will always be moving away from each other.We know the distance between the ants at three moments in time. Note that between the first and second moment, 2 minutes have passed, and the distance between the ants has decreased by 4 meters. Between the second and third moment, 4 minutes have passed, and the distance has decreased by 2 meters. Since the distance decreased both times, we can be sure that 3 minutes and 5 minutes after the start of the observation, the ants were not in a "moving away" state, meaning they could only be in states 1 or 3.If the meeting between them had not occurred in the next 4 minutes (from the 5th to the 9th minute), they would have remained in the same state (1 or 3) and continued to approach each other at a rate of 4 meters in 2 minutes, meaning they should have closed the distance by 8 meters in 4 minutes. However, the distance between them decreased by only 2 meters, so at some point between the 2nd and 3rd moments, a meeting must have occurred.After the meeting, the ants move away from each other at the same speed they approached (in situations 1 and 2, the speeds of approaching and moving away are equal to the sum of the ants' speeds, while in situations 3 and 4, they are equal to the difference in their speeds). Therefore, in 4 minutes, the distance between the ants decreased from 5 meters to zero and then increased from zero to 3 meters. In total, 8 meters in 4 minutes, which matches the previously found rate of approaching. One minute earlier, the distance was 2 meters less. Therefore, 8 minutes after the start of the movement, the distance between the ants was 1 meter.

answer:[Solution] From the given, if a>0, we have b-a leqslant a sin x+b leqslant a+b, which implies left{begin{array}{l}b+a=1, b-a=-7 .end{array}right. Solving this, we get quadleft{begin{array}{l}a=4, b=-3 .end{array}right.If a<0, we have quad b+a leqslant a sin x+b leqslant b-a, which implies left{begin{array}{l}b-a=1, b+a=-7 .end{array}right. Solving this, we get quadleft{begin{array}{l}a=-4, b=-3 .end{array}right.Let g(x)=b sin ^{2} x-a cos ^{2} x. Then, when a=4, b=-3, g(x)=-3 sin ^{2} x-4 cos ^{2} x=-3-cos ^{2} x leqslant-3,Thus,g(x)_{max }=-3 text {. }When a=-4, quad b=-3,g(x)=-3 sin ^{2} x+4 cos ^{2} x=4-7 sin ^{2} x leqslant 4,Thus,g(x)_{max }=4 text {. }Therefore, the answer is (mathrm{C}).