answer:1. Understanding the problem: We need to find the largest integer ( n ) such that for any set of 2000 points ({(x_1, y_1), (x_2, y_2), ldots, (x_{2000}, y_{2000})}) where (0 leq x_i leq 83), (0 leq y_i leq 1), and (x_i neq x_j) for (i neq j), there exists a unit square that contains exactly ( n ) of these points.2. Visualizing the problem: The points are distributed in a rectangle of width 83 and height 1. Since ( x_i neq x_j ) for ( i neq j ), each ( x_i ) is unique and lies between 0 and 83. The ( y_i ) values are between 0 and 1.3. Dividing the rectangle: Consider dividing the rectangle into vertical strips of width 1. There are 83 such strips, each of width 1 and height 1.4. Distributing points: Since there are 2000 points and 83 strips, by the pigeonhole principle, at least one strip must contain at least: [ leftlceil frac{2000}{83} rightrceil = 25 text{ points} ] This is because ( leftlceil frac{2000}{83} rightrceil ) is the smallest integer greater than or equal to ( frac{2000}{83} ).5. Ensuring the maximum ( n ): We need to ensure that there is a unit square that contains exactly ( n ) points. Since each strip is of width 1 and height 1, and we have at least one strip containing 25 points, we can conclude that the largest ( n ) such that any good set of points will have a unit square containing exactly ( n ) points is 25.The final answer is ( boxed{25} ).

answer: Solution:# Part (1):Given the function f(x)=frac{sqrt{3}}{2}sinomega x-frac{1}{2}cosomega x-m, we can rewrite it as:[f(x)=sin(omega x-frac{pi}{6})-m]For the maximum value of f(x), we set sin(omega x-frac{pi}{6})=1, which gives:[f(x)_{max }=1-m]For the minimum value of f(x), we set sin(omega x-frac{pi}{6})=-1, which results in:[f(x)_{min }=-1-m]Given that the maximum value is 5 times the minimum value, we have:[1-m=5(-1-m)]Solving for m, we get:[1-m=-5-5m][4m=-6][m=-frac{3}{2}]Therefore, the value of m is boxed{m=-frac{3}{2}}.# Part (2):When m=frac{sqrt{2}}{2}, the function becomes:[f(x)=sin(omega x-frac{pi}{6})-frac{sqrt{2}}{2}]Setting f(x)=0, we have:[sin(omega x-frac{pi}{6})=frac{sqrt{2}}{2}]This equation gives us two possibilities:[omega x-frac{pi}{6}=2kpi+frac{pi}{4}][omega x-frac{pi}{6}=2kpi+frac{3pi}{4}] where kinmathbb{Z}.Solving for x in both cases, we get:[x=frac{2kpi+frac{5pi}{12}}{omega}][x=frac{2kpi+frac{11pi}{12}}{omega}] where kinmathbb{Z}.Taking k=0, we find the first two positive zeros:[x_{1}=frac{5pi}{12omega}][x_{2}=frac{11pi}{12omega}]Given that {x}_{2}-2{x}_{1}=frac{pi}{36}, we substitute the values of x_1 and x_2:[frac{11pi}{12omega}-2left(frac{5pi}{12omega}right)=frac{pi}{36}]Simplifying, we get:[frac{11pi}{12omega}-frac{10pi}{12omega}=frac{pi}{36}][frac{pi}{12omega}=frac{pi}{36}]Solving for omega, we find:[12omega=36][omega=3]Thus, the value of omega is boxed{omega=3}.

answer:1. To find the value of ( n ) that minimizes the expression ( S = |n-1| + |n-2| + ldots + |n-100| ), we need to consider the properties of absolute values and the sum of absolute deviations.2. The sum of absolute deviations ( S ) is minimized when ( n ) is the median of the set of numbers ({1, 2, ldots, 100}). This is because the median minimizes the sum of absolute deviations from a set of numbers.3. The set ({1, 2, ldots, 100}) has 100 elements. For an even number of elements, the median is the average of the two middle numbers. The two middle numbers in this set are 50 and 51.4. Therefore, the median of the set ({1, 2, ldots, 100}) is: [ text{Median} = frac{50 + 51}{2} = frac{101}{2} = 50.5 ]5. Since ( n ) must be an integer, we consider the integers closest to 50.5, which are 50 and 51.6. We need to check the values of ( S ) for ( n = 50 ) and ( n = 51 ): - For ( n = 50 ): [ S = |50-1| + |50-2| + ldots + |50-100| ] This simplifies to: [ S = 49 + 48 + ldots + 0 + 1 + 2 + ldots + 50 ] The sum of the first 49 positive integers is: [ sum_{k=1}^{49} k = frac{49 cdot 50}{2} = 1225 ] The sum of the first 50 positive integers is: [ sum_{k=1}^{50} k = frac{50 cdot 51}{2} = 1275 ] Therefore, for ( n = 50 ): [ S = 1225 + 1275 = 2500 ] - For ( n = 51 ): [ S = |51-1| + |51-2| + ldots + |51-100| ] This simplifies to: [ S = 50 + 49 + ldots + 1 + 0 + 1 + ldots + 49 ] The sum of the first 50 positive integers is: [ sum_{k=1}^{50} k = frac{50 cdot 51}{2} = 1275 ] The sum of the first 49 positive integers is: [ sum_{k=1}^{49} k = frac{49 cdot 50}{2} = 1225 ] Therefore, for ( n = 51 ): [ S = 1275 + 1225 = 2500 ]7. Both ( n = 50 ) and ( n = 51 ) yield the same minimum value for ( S ).The final answer is ( boxed{ n = 50 } ) or ( n = 51 ).

answer:Method 1: Algebraic Method For line l: rhocostheta-rhosintheta+1=0 Rightarrow x-y+1=0, For curve C: begin{cases} x= sqrt {2}costheta y= sqrt {2}sintheta end{cases} Rightarrow x^{2}+y^{2}=2, By combining, begin{cases} y=x+1 x^{2}+y^{2}=2 end{cases}, we get x^{2}+(x+1)^{2}-2=0, That is 2x^{2}+2x-1=0, let A(x_{1},y_{1}), B(x_{2},y_{2}), By Vieta's formulas, begin{cases} x_{1}+x_{2}=-1 x_{1}x_{2}=- frac {1}{2} end{cases}, Thus, |AB|= sqrt {1+k^{2}}|x_{1}-x_{2}| = sqrt {1+k^{2}} sqrt {(x_{1}+x_{2})^{2}-4x_{1}x_{2}} = sqrt {6}, choose boxed{text{D}}. Method 2: Geometric Method For line l: rhocostheta-rhosintheta+1=0 Rightarrow x-y+1=0, For curve C: begin{cases} x= sqrt {2}costheta y= sqrt {2}sintheta end{cases} Rightarrow x^{2}+y^{2}=2, The distance d from the center (0,0) to the line x-y+1=0 is d= frac {1}{ sqrt {2}}= frac { sqrt {2}}{2}, The radius r= sqrt {2}, thus |AB|=2 sqrt {r^{2}-d^{2}}= sqrt {6}, choose boxed{text{D}}. Note: Of course, this problem can also be directly solved by finding the coordinates of points A and B, and then using the distance formula between two points. First, convert the polar equation of the line into a rectangular coordinate equation, and the parametric equation of curve C into a standard equation, then solve using either the algebraic method or geometric method. Converting polar coordinates and parametric equations into familiar rectangular coordinate problems is key to solving these types of problems.

answer:Solution. Triangles ABC and ABD have equal areas because they have a common base and equal heights. Therefore, fromP_{AOD} = P_{ABD} - P_{1} quad P_{BCO} = P_{ABC} - P_{1}we getP_{ADO} = P_{BCO} = P_{3}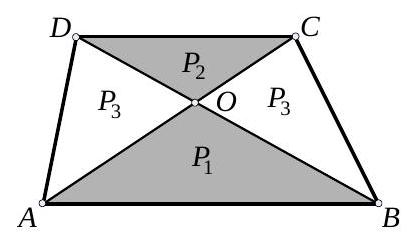Since triangles ADO and ABO have equal heights, the ratio of their areas is equal to the ratio of their bases, i.e.,P_{3} : P_{1} = overline{OD} : overline{OB}Similarly, for the areas of triangles CDO and CBO, we haveP_{2} : P_{3} = overline{OD} : overline{OB}From (1) and (2), we get P_{3} = sqrt{P_{1} P_{2}}, so for the area of the trapezoid, we haveP = P_{1} + 2P_{3} + P_{2} = P_{1} + 2sqrt{P_{1} P_{2}} + P_{2} = left(sqrt{P_{1}} + sqrt{P_{2}}right)^{2}

answer:［Solution］ By Cauchy-Schwarz inequality, we haveleft|x sqrt{1-y^{2}}+y sqrt{1-x^{2}}right|^{2} leqslantleft(x^{2}+y^{2}right)left(2-x^{2}-y^{2}right) .Using the AM-GM inequality, we getleft|x sqrt{1-y^{2}}+y sqrt{1-x^{2}}right| leqslant frac{x^{2}+y^{2}+2-x^{2}-y^{2}}{2}=1 .If x=frac{1}{2}, y=frac{sqrt{3}}{2}, thenx sqrt{1-y^{2}}+y sqrt{1-x^{2}}=1 .Therefore, the maximum value sought is 1 .