Appearance
question:4 cdot 31 Solve the equation left[x^{2}-2 xright]=[x]^{2}-2[x] for real numbers.Find the real solutions to the equation left[x^{2}-2 xright]=[x]^{2}-2[x].
answer:[Solution] Let y=x-1, then left[y^{2}right]=[y]^{2}.If y geqslant 0, then y^{2} geqslant[y]^{2}>y^{2}-1.So [y] leqslant y<sqrt{1+[y]^{2}}.That is, x inleft[n+1,1+sqrt{1+n^{2}}right), for any n in N cup{0}.If y<0, then [y]^{2} geqslant y^{2} geqslantleft[y^{2}right],So y must be an integer to have left[y^{2}right]=[y]^{2}, that is, x is a negative integer or 0.
question:12. Given three spheres with a radius of 6 on the same side of plane a, all tangent to plane alpha, and each sphere is externally tangent to the other two, there is another sphere that is tangent to plane alpha and these three spheres. Then its radius is qquad
answer:12. 2.The above text has been translated into English, retaining the original text's line breaks and formatting. Here is the direct output of the translation result. However, the original text "12. 2." is a number and does not have a meaningful translation, so it remains unchanged.
question:Given the curve y= frac{x^{2}}{4}-ln x, the slope of one of its tangent lines is (-frac{1}{2}). Find the coordinates of the point of tangency.
answer:From y= frac{x^{2}}{4}-ln x we get y'= frac{1}{2}x-frac{1}{x}.Let (x_{0}, y_{0}) be the point of tangency of the tangent line with slope (-frac{1}{2}), (x_{0} > 0).Then frac{1}{2}x_{0}-frac{1}{x_{0}}=-frac{1}{2}.Solving this equation gives x_{0}=1.Therefore, y_{0}=frac{1}{4}.Hence, the point of tangency is boxed{(1, frac{1}{4})}.To find the point of tangency, we first compute the derivative of the given function. We then set the derivative equal to the given slope (-frac{1}{2}) and solve for x_{0}. We discard any solutions for x_{0} that are not in the domain of the function. Finally, we find y_{0} by substituting the obtained x_{0} value into the original function.This problem tests your understanding of using derivatives to find the slope of a tangent line to a curve at a given point, as well as basic differentiation formulas for elementary functions. It is of moderate difficulty.
question:A jacket was initially marked up by 50% of its cost price and then sold at a discount of 20% off the marked price, resulting in a profit of 28 yuan. If we let the cost price of the jacket be x yuan, then the correct equation according to the problem is ( )A: 0.8(1+0.5)x=x+28B: 0.8(1+0.5)x=x-28C: 0.8(1+0.5x)=x-28D: 0.8(1+0.5x)=x+28
answer:Let the cost price of the jacket be x yuan.According to the problem, 0.8(1+50%)x-x=28,which simplifies to 0.8(1+0.5)x=28+x.Therefore, the correct option is boxed{A}.Analysis: Let the cost price of the jacket be x yuan. According to the problem, the profit can be calculated as the selling price (80% of the marked price) minus the cost price. Based on this, we can set up the equation.
question:5. The quadrilateral formed by connecting the midpoints of the four sides of an isosceles trapezoid in sequence is ( ).mathrm{A}, parallelogram, mathrm{B}, rectangle, mathrm{C}, rhombus, mathrm{D}, square.
answer:5. (C)Translate the text above into English, please retain the original text's line breaks and format, and output the translation result directly.
question:Florinda went for a walk. She left point A and walked 1 mathrm{~m}. At this point, she turned left at an angle of 90^{circ} and walked 2 mathrm{~m}. At the last point, she turned left again and walked 3 mathrm{~m}. She continued walking in this manner until, on the last segment, she walked 30 mathrm{~m} and reached her final point, which we will call point B. The following figure illustrates the first seven segments of Florinda's walk (note that point B is not illustrated).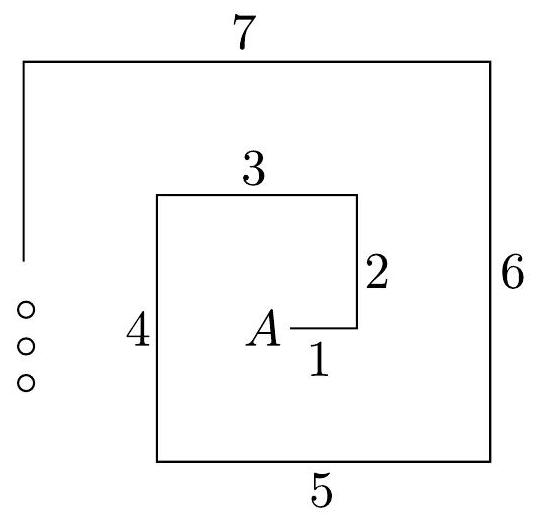Calculate the distance between points A and B.#
answer:SolutionIn this exercise, all distances are given in meters. Observe in the following figure that the horizontal straight-line segments have odd lengths while the vertical ones have even lengths.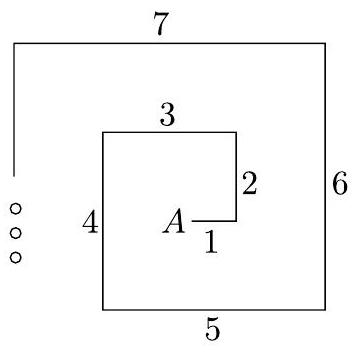If we consider only the horizontal straight-line segments, we obtain that the total horizontal displacement is equal to1-3+5-7+9-11+13-cdots+25-27+29To calculate this value, we can group the terms as follows:1 underbrace{-3+5}_{+2} underbrace{-7+9}_{+2} underbrace{-11+13}_{+2}-ldots underbrace{-27+29}_{+2}The total horizontal displacement is, then, equal to 1+2 times 7=15.Now considering the vertical displacements and calculating similarly, we obtain2 underbrace{-4+6}_{+2} underbrace{-8+10}_{+2} underbrace{-12+14}_{+2}-ldots underbrace{-28+30}_{+2}=2+2 times 7=16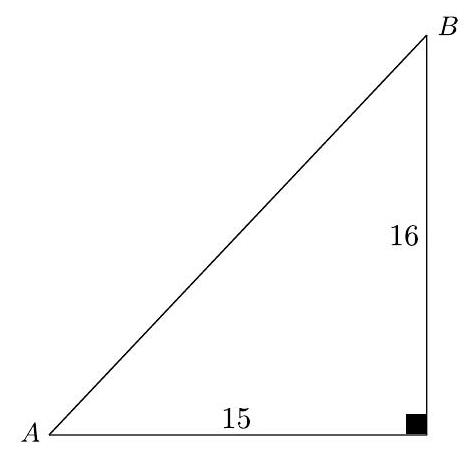Finally, by the Pythagorean Theorem, we conclude that the total displacement is equal tosqrt{15^{2}+16^{2}}=sqrt{481}