answer:16. D.Consider any point P(x, y) on the coordinate plane. The point symmetric to P with respect to the x-axis is P^{prime}(x,-y). Then, rotating point P^{prime} counterclockwise by 90^{circ} around the origin O, we get P^{prime prime}(y, x). Therefore, P and P^{prime prime} are symmetric with respect to the line y=x.

answer: Step-by-Step Solution# Part (1): Finding the value of aGiven the function f(x)=log_{2}left(frac{2}{{x-1}}+aright) is an odd function, we have the property that f(x) + f(-x) = 0. This implies:[log_{2}left(frac{2}{{x-1}}+aright) + log_{2}left(frac{2}{{-x-1}}+aright) = 0]Using the property of logarithms that log_b(m) + log_b(n) = log_b(mn), we get:[log_{2}left((frac{2}{{x-1}}+a)(frac{2}{{-x-1}}+a)right) = 0]This implies that:[(frac{2}{{x-1}}+a)(frac{2}{{-x-1}}+a) = 1]Expanding and simplifying, we find:[left(2-aright)^{2}-a^{2}x^{2}=1-x^{2}]This leads to a system of equations:[left{begin{array}{l}{(2-a)^{2}=1}{-a^{2}=-1}end{array}right.]Solving this system, we find a=1. Thus, the value of a that makes f(x) an odd function is:[boxed{a=1}]# Part (2): Finding the range of real number bGiven f(x)=log_{2}frac{x+1}{x-1}, the domain of f(x) is left(-infty ,-1right)cup left(1,+infty right). This implies 2^{x} > 1 or 2^{x} 0.Considering the inequality 2^{f(2^{x})}+3cdot 2^{x}-bgeqslant 0, we find that:[bleqslant frac{{2}^{x}+1}{{2}^{x}-1}+3cdot 2^{x}]Simplifying, we get:[bleqslant 3(2^{x}-1)+frac{2}{{2}^{x}-1}+4]Using the AM-GM inequality, we find that:[3(2^{x}-1)+frac{2}{{2}^{x}-1}geqslant 2sqrt{[3({2}^{x}-1)]timesfrac{2}{{2}^{x}-1}}=2sqrt{6}]Thus, the minimum value of 3(2^{x}-1)+frac{2}{{2}^{x}-1}+4 is 2sqrt{6}+4. Therefore, the range of real number b is:[boxed{(-infty, 2sqrt{6}+4]}]

answer:Given the conditions a > 0, b > -1, and a+b=1, we are asked to find the minimum value of the expression frac{1}{a} + frac{1}{b+1}. Firstly, we note that since a > 0 and b > -1, it follows that b+1 > 0. This is because adding 1 to a number greater than -1 will always result in a positive number. Next, we can rewrite the given expression by incorporating the condition a + b = 1:begin{align*}frac{1}{a} + frac{1}{b+1} & = frac{1}{2}left(frac{1}{a} + frac{1}{b+1}right)(a + b + 1) & = frac{1}{2}left(frac{b+1}{a} + frac{a}{b+1} + 2right).end{align*}At this point, we can apply the AM-GM inequality (Arithmetic Mean-Geometric Mean inequality), which states that for any non-negative real numbers x and y, the inequality frac{x+y}{2} geq sqrt{xy} holds, where equality occurs if and only if x = y.Applying AM-GM to frac{b+1}{a} and frac{a}{b+1}, we get:begin{align*}frac{1}{2}left(frac{b+1}{a} + frac{a}{b+1} + 2right) & geq frac{1}{2}(2sqrt{frac{b+1}{a} cdot frac{a}{b+1}} + 2) & = frac{1}{2}cdot(2cdot1 + 2) & = 2.end{align*}Equality holds when frac{b+1}{a} = frac{a}{b+1}, which, given the constraint a + b = 1, occurs when a = 1 and b = 0.Therefore, the minimum value of frac{1}{a} + frac{1}{b+1} is boxed{2}.

answer:You can see that since the ratio of real building's heights to the model building's height is 1:20. We also know that the U.S Capitol is 289 feet in real life, so to find the height of the model, we divide by 20. That gives us 14.45 which rounds to 14. Therefore, to the nearest whole number, the duplicate is boxed{textbf{(A) }14}. ~avamarora, Nivaar.

answer:To simplify and then evaluate the given expression under the constraints of the inequality system, we proceed as follows:Step 1: Simplify the given expressionbegin{align*}left(1+frac{3x-1}{x+1}right)÷frac{x}{x^{2}-1} &= frac{x+1+3x-1}{x+1}•frac{x^{2}-1}{x} &= frac{4x}{x+1}•frac{(x+1)(x-1)}{x} &= 4(x-1) &= 4x-4.end{align*}Step 2: Solve the inequality systemGiven the system:[left{begin{array}{l}1-x>frac{-1-x}{2} x+1>0end{array}right.]For the first inequality:begin{align*}1-x &> frac{-1-x}{2} 2(1-x) &> -1-x 2-2x &> -1-x x &0 implies x>-1.]Therefore, the solution set for the inequality system is -1 < x < 3.Step 3: Find the integer solutionsThe integer solutions within the range -1 < x < 3 are 0, 1, and 2.Step 4: Evaluate the expression for valid integer solutionsThe expression becomes meaningless for x=1 and x=0 because the denominator in the original expression becomes 0. Thus, the only valid integer solution is x=2.Step 5: Substitute x=2 into the simplified expression[4x-4 = 4(2)-4 = 8-4 = 4.]Therefore, the evaluated expression, under the given constraints, is boxed{4}.

answer:First note that since 3^{2}+4^{2}=5^{2}, we have angle B=90^{circ} by the (converse to the) Pythagorean theorem. We calculate the area of the triangle in two ways. Viewing A B as the base and B C as the height, we get that the area is frac{1}{2} cdot 3 cdot 4=6. But viewing A C as the base and h (the distance to be determined) as the height, we get an equation: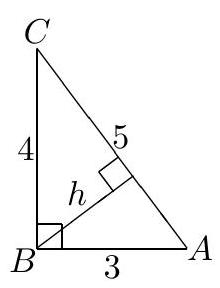begin{aligned}frac{1}{2} cdot 5 cdot h & =6 frac{5}{2} cdot h & =6 frac{2}{5} cdot frac{5}{2} cdot h & =6 cdot frac{2}{5} h & =frac{6 cdot 2}{5}=frac{12}{5} .end{aligned}