answer:## Solution.Leta_{n}=lfloorsqrt[4]{1}rfloor+lfloorsqrt[4]{2}rfloor+ldots+lfloorsqrt[4]{n}rfloorWe need to solve the equationa_{n}=frac{3}{2} n+1Note that lfloorsqrt[4]{k}rfloor=1 for 1 leqslant k<16.Therefore, for 1 leqslant n leqslant 15, we have a_{n}=n.Among these numbers, there are no numbers for which the given equality holds.The equality lfloorsqrt[4]{k}rfloor=2 holds for 16 leqslant k<81.Therefore, for 16 leqslant n leqslant 80, we have a_{n}=1+1+ldots+1+2+ldots+2=15+2 cdot(n-15)=2 n-15. 1 pointFor 16 leqslant n leqslant 80 to satisfy equation (*), it must be that 2 n-15=frac{3}{2} n+1.We get one solution n=32, and this is the only solution of the problem less than 81.1 pointThere are no other (larger) solutions, because after n=81, with each increase of n by 1, the value of the left side increases by at least 3, while the value on the right side increases by frac{3}{2}, so the left side will remain greater than the right side.

answer:## SolutionBy definition, the derivative at the point x=0:f^{prime}(0)=lim _{Delta x rightarrow 0} frac{f(0+Delta x)-f(0)}{Delta x}Based on the definition, we find:begin{aligned}& f^{prime}(0)=lim _{Delta x rightarrow 0} frac{f(0+Delta x)-f(0)}{Delta x}=lim _{Delta x rightarrow 0}left(e^{sin left(Delta x^{frac{3}{2}} sin frac{2}{Delta x}right)}-1+Delta x^{2}-0right) / Delta x= & =lim _{Delta x rightarrow 0}left(e^{sin left(Delta x^{frac{3}{2}} sin frac{2}{Delta x}right)}-1+Delta x^{2}right) / Delta x= & =lim _{Delta x rightarrow 0}left(e^{sin left(Delta x^{frac{3}{2}} sin frac{2}{Delta x}right)}-1right) / Delta x+lim _{Delta x rightarrow 0} frac{Delta x^{2}}{Delta x}=end{aligned}Using the substitution of equivalent infinitesimals:e^{sin left(Delta x^{frac{3}{2}} sin frac{2}{Delta x}right)}-1 sim sin left(Delta x^{frac{3}{2}} sin frac{2}{Delta x}right) text{, as } Delta x rightarrow 0left(sin left(Delta x^{frac{3}{2}} sin frac{2}{Delta x}right) rightarrow 0right)We get:=lim _{Delta x rightarrow 0} frac{sin left(Delta x^{frac{3}{2}} sin frac{2}{Delta x}right)}{Delta x}+lim _{Delta x rightarrow 0} Delta x=Using the substitution of equivalent infinitesimals: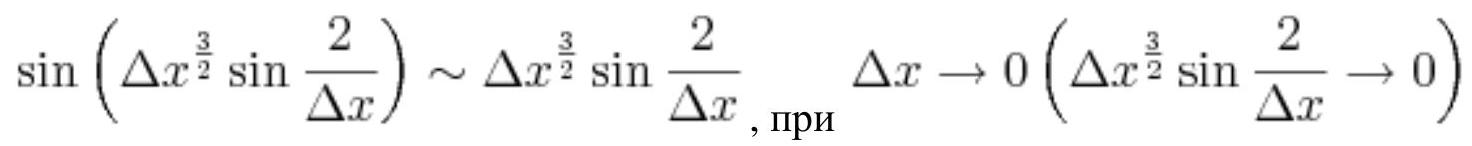We get:=lim _{Delta x rightarrow 0} frac{Delta x^{frac{3}{2}} sin frac{2}{Delta x}}{Delta x}+0=lim _{Delta x rightarrow 0} Delta x^{frac{1}{2}} sin frac{2}{Delta x}=Since sin frac{2}{Delta x} is bounded, thenDelta x^{frac{1}{2}} cdot sin frac{2}{Delta x} rightarrow 0 text{, as } Delta x rightarrow 0left(Delta x^{frac{1}{2}} rightarrow 0right)Thus,=0Therefore, f^{prime}(0)=0Problem Kuznetsov Differentiation 2-26

answer:Alice may sit in the center chair, in an end chair, or in a next-to-end chair. Suppose she sits in the center chair. The 2nd and 4th chairs (next to her) must be occupied by Derek and Eric, in either order, leaving the end chairs for Bob and Carla in either order; this yields 2! * 2! = 4 ways to seat the group.Next, suppose Alice sits in one of the end chairs. Then the chair beside her will be occupied by either Derek or Eric. The center chair must be occupied by Bob or Carla, leaving the last two people to fill the last two chairs in either order. 2 ways to seat Alice times 2 ways to fill the next chair times 2 ways to fill the center chair times 2 ways to fill the last two chairs yields 2 * 2 * 2 * 2 = 16 ways to fill the chairs.Finally, suppose Alice sits in the second or fourth chair. Then the chairs next to her must be occupied by Derek and Eric in either order, and the other two chairs must be occupied by Bob and Carla in either order. This yields 2 * 2 * 2 = 8 ways to fill the chairs. In total, there are 4 + 8 + 16 ways to fill the chairs, so the answer is boxed{bold{(C)} 28}.

answer:Solution: For proposition p: There exists x_0 in mathbb{R}, such that x_0 - 2 > 0. For example, take x_0 = 3, which makes it a true proposition.For proposition q: For all x in mathbb{R}, 2^x > x^2, this is a false proposition. For example, take x = 2.Therefore, among the propositions listed, the true proposition is p ∧ (¬q).Hence, the correct choice is: boxed{text{C}}.First, determine the truth of the compound propositions p and q, then use the method of determining the truth of compound propositions to obtain the result.This question examines the method of simple logic determination, properties of functions, and tests reasoning and computational abilities.

answer:Let's first find the two roots of the quadratic equation x^2 - 17x + 60 = 0. To do this we can factor the equation as follows:x^2 - 17x + 60 = (x - 5)(x - 12) = 0.Therefore, we have two roots:x = 5 quad text{or} quad x = 12.Since the triangle is right-angled, we can assume either of these roots can serve as one of the non-hypotenuse sides. Let's explore both cases.Case 1: If the longer side is the hypotenuse.We have one side of the triangle being 12 and the other being 5. Using the Pythagorean theorem to find the hypotenuse (let's denote this as c), we have:c^2 = 5^2 + 12^2,c^2 = 25 + 144,c^2 = 169,c = sqrt{169},c = 13.Therefore, the length of the hypotenuse is boxed{13} when the side with length 12 is not the hypotenuse.Case 2: If the longer side is not the hypotenuse.Here, we know that the hypotenuse is longer than either of the other two sides, so there is no valid triangle where the side of length 12 is a non-hypotenuse side and the side with length 5 is the hypotenuse, as the sum of the squares of both non-hypotenuse sides must equal the square of the hypotenuse. Therefore, the only valid case is the aforementioned case where the hypotenuse is 13.

answer:Since |AF|=4, by the definition of a parabola,- The distance from point A to the directrix is 4, meaning the x-coordinate of point A is -2.- As point A is on the parabola, its coordinates are A(-2, 4).- The coordinates of the origin's symmetric point with respect to the directrix are B(4, 0).Thus, the minimum value of |PA|+|PO| is:- |AB| = sqrt{(4+2)^{2}+(0-4)^{2}} = 2sqrt{13}.Hence, the answer is boxed{2sqrt{13}}.This problem tests the student's ability to flexibly use the simple properties of parabolas to solve minimum value problems and to simplify calculations using point-to-point distance and symmetry. It is a moderate-level question.