Appearance
question:11.056. The diagonal of a rectangular parallelepiped is 10 cm and forms an angle of 60^{circ} with the base plane. The area of the base is 12 mathrm{~cm}^{2}. Find the lateral surface area of the parallelepiped.
answer:Solution.From triangle D_{1} D B (Fig. 11.51) we find B D=5 text{ cm}, D D_{1}=5 sqrt{3} text{ cm}. The lateral surface area S_{text {lateral }}=2left(D D_{1} cdot D C+D D_{1} cdot A Dright)=2 D D_{1}(D C+A D). But D C^{2}+A D^{2}= =B D^{2}=25, and by the condition D C cdot A D=12. Therefore, (D C+A D)^{2}= =D C^{2}+A D^{2}+2 D C cdot A D=25+24=49, from which D C+A D=7 (cm). Thus, S_{text {lateral }}=2 cdot 5 sqrt{3} cdot 7=70 sqrt{3}left(text{cm}^{2}right).Answer: 70 sqrt{3} text{ cm}^{2}.
question:When Yunji added all the integers from 1 to 9, she mistakenly left out a number. Her incorrect sum turned out to be a square number. What number did Yunji leave out?
answer:The sum of digits 1-9 is 45, 45-9=36 36=6^2 Therefore, the solution is that the integer she forgot was 9.
question:In a 3 times 3 table, we placed a 1-forint coin heads up in each cell. What is the minimum number of coins we need to flip so that there are neither three heads nor three tails in a row (row, column, diagonal)?
answer:Solution. Consider three rows of the table. They have no common part, and each of them must contain at least one head. This means that we must flip at least 3 coins, and these must be placed in different rows and, similarly, in different columns. If there were no heads in any corner, then only the positions marked on the 1st figure could be considered; however, it is not possible to choose three of these so that they are all in different rows and different columns. Therefore, there must be a head in one of the corners; let it be, for example, the top left.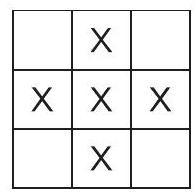Figure 1According to the requirement of different rows and columns, in this case, the other two heads can only be placed in two ways (cases 1 and 2, Figure 2). It can be seen that in case 1, three heads fall on a diagonal, and in case 2, one diagonal remains all tails; thus, flipping 3 coins is not enough, at least 4 are needed. However, 4 is sufficient, a possible arrangement is shown in Figure 3.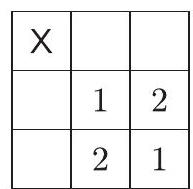Figure 2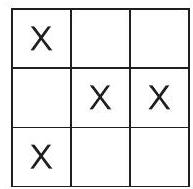Figure 3We can generalize the problem to an n times n table instead of a 3 times 3 one, where n geq 4. In this case, for n geq 4, it is sufficient to flip n coins; a suitable choice is shown in Figure 4.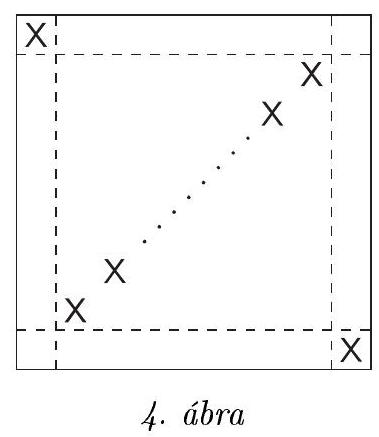
question:Let f(x)=ae^{x}(x+1) (where e is the base of natural logarithm) and g(x)=x^{2}+bx+2. It is known that they have the same tangent line at x=0. (Ⅰ) Find the analytical expressions for functions f(x) and g(x). (Ⅱ) Find the minimum value of function f(x) on the interval left[t,t+1right] where t>-3. (Ⅲ) If for all xgeqslant -2, kf(x) > g(x) always holds, find the range of real number k.
answer:Let's break down the solution step by step according to the rules: (Ⅰ) Analytical Expressions for f(x) and g(x)- First, we find the derivatives of f(x) and g(x):f'(x) = ae^x(x+2),quad g'(x) = 2x+b- At x=0, the derivatives become:f'(0) = 2a,quad g'(0) = b- Since f(x) and g(x) have the same tangent line at x=0, it means:2a = b,quad f(0) = a = g(0) = 2- Solving these equations, we get:a = 2,quad b = 4- Therefore, the analytical expressions are:boxed{f(x) = 2e^x(x+1),quad g(x) = x^2 + 4x + 2} (Ⅱ) Minimum Value of f(x) on Interval [t, t+1]- The derivative of f(x) is:f'(x) = 2e^x(x+2)- Analyzing the sign of f'(x): - f'(x) > 0 for x > -2 - f'(x) -3, and t + 1 > -2: - For -3 0 for x geq -2. Since F(0) = 2k - 2 > 0, we get:k > 1- The derivative of F(x) is:F'(x) = 2(x+2)(ke^x - 1)- Analysis of F'(x) shows F(x) has one extremum at x = lnfrac{1}{k}: 1. Case 1: k > e^2, makes F(x)_{min} 0, satisfying the condition.- Therefore, the range of k is:boxed{k in (1, e^2)}
question:10. As shown in the figure, there is a cubic wooden block with a side length of 5 cm. A small cube with a side length of 1 cm is removed from each corner, each edge, and the center of each face (i.e., the small cubes shaded in the figure). What is the remaining surface area in square centimeters?
answer:【Analysis】The original surface area is 150. If a part is removed from a corner, the surface area remains unchanged; if a part is removed from an edge, the surface area increases by 2; if a part is removed from a face, the surface area increases by 4. Therefore, the remaining surface area is 150+2 times 12+4 times 6=198.
question:If the line ax+2y+6=0 and the line x+a(a+1)y+(a^2-1)=0 are perpendicular, then the value of a is ( )A: -frac{3}{2} or 0 B: 0 C: -frac{2}{3} or 0 D: -3
answer:To solve this, we consider the lines ax+2y+6=0 and x+a(a+1)y+(a^2-1)=0 being perpendicular. When a=0, it is obviously true; When aneq0, we have - frac{a}{2}(- frac{1}{a(a+1)}) =-1 Solving this gives a=-frac{3}{2} Therefore, the correct choice is boxed{text{A}}. For two lines to be perpendicular, we first consider the case where the slope is 0; if the slope is not 0, the product of the slopes is -1. By solving for a, we obtain the options. This question tests the determination of perpendicular lines and the ability to analyze and solve problems, making it a basic question.