answer:2. A.M cap N neq varnothing is equivalent to the point (0, b) being on or inside the ellipse frac{x^{2}}{3}+frac{2 y^{2}}{3}=1, so frac{2 b^{2}}{3} leqslant 1. Therefore, -frac{sqrt{6}}{2} leqslant b leqslant frac{sqrt{6}}{2}.

answer:## SolutionLet's find the vector overrightarrow{B C}:overrightarrow{B C}={-3-(-4) ; 2-0 ; 5-3}={1 ; 2 ; 2}Since the vector overrightarrow{B C} is perpendicular to the desired plane, it can be taken as the normal vector. Therefore, the equation of the plane will be:begin{aligned}& (x-(-3))+2 cdot(y-5)+2 cdot(z-(-2))=0 & x+3+2 y-10+2 z+4=0 & x+2 y+2 z-3=0end{aligned}## Problem Kuznetsov Analytic Geometry 9-6

answer:4. The center S of the circle circumscribed around the rectangle is also the midpoint of the diagonal A C, so Sleft(frac{x_{A}+x_{C}}{2}, frac{y_{A}+y_{C}}{2}right) or Sleft(-frac{1}{2}, 1right). From the sketch, it is clear that the radius R is equal to half the length of the diagonal A C. Since |A C|= sqrt{left(x_{C}-x_{A}right)^{2}+left(y_{C}-y_{A}right)^{2}}=sqrt{9+16}=5, it follows that R=frac{5}{2}.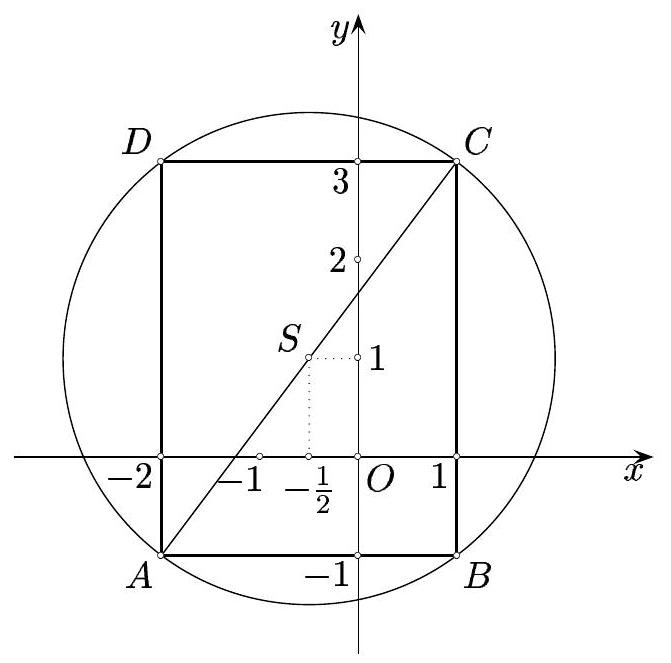SketchCalculated coordinates of the center: Sleft(-frac{1}{2}, 1right) 1 point 1 pointConclusion R=frac{1}{2} cdot d(A, C) or R=frac{1}{2} cdot|A C|.1 pointWriting or using the distance formula between points......................................................................................Correctly substituting the data into the formula ........................................................................

answer:Answer: 1.5 | 3 / 2Allowed for input are digits, minus, and division sign, a dot or comma as a decimal separator, a semicolon#

answer:Answer: 10 packages, 5 candies.Solution. Let's number the gifts from the smallest to the largest, from 1 to n. If the third gift has 7 or fewer candies, then the three smallest gifts have no more than 7+6+5=18 candies. This contradicts the condition. Therefore, the third gift has at least 8 candies. Similarly, the third from the last gift has no more than 15 candies (16+17+18=51>50).Remove the three largest and the three smallest gifts. In the remaining gifts, there will be 115 - 20 50=45 candies, and each will have between 9 and 14 candies. Three packages are clearly not enough ( 14+13+12=39 ), and five would be too many ( 9+10+11+12+13=55 ). Therefore, 45 candies are distributed in 4 packages. This is possible: 47=9+11+12+13. Note that the fourth package cannot have more than 9 candies: 10+11+12+13=46>45.If the fourth package has 9 candies, then the third has no more than 8, the second no more than 7, so the first package has at least 20-8-7=5 candies. But no more, since 6+7+8=21.Criteria. Only the answer - 0 points. Only correct estimates for a_{3} and a_{n-3}-3 points. Only a justified answer for the number of packages - 5 points. Full solution - 7 points.

answer:Problem 4. Let2^{x}=left(1+operatorname{tg} 0.01^{circ}right)left(1+operatorname{tg} 0.02^{circ}right)left(1+operatorname{tg} 0.03^{circ}right) ldotsleft(1+operatorname{tg} 44.99^{circ}right)Find x. If necessary, round your answer to 0.01.Answer: 2249.5.