Appearance
question:Problem 8.2.1. Given trapezoid A B C D(A D | B C). It turns out that angle A B D=angle B C D. Find the length of segment B D, if B C=36 and A D=64.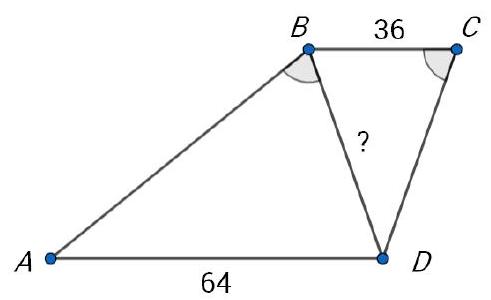
answer:Answer: 48.Solution. Since A D | B C, we have angle C B D=angle B D A. Then triangles A B D and D C B are similar by the first criterion. Therefore, frac{64}{B D}=frac{A D}{B D}=frac{B D}{B C}=frac{B D}{36}, from which we find B D=sqrt{64 cdot 36}=48.
question:If 0 < x < frac{pi}{2} and frac{sin x}{1 + cos x} = frac{1}{3}, what is frac{sin 2x}{1 + cos 2x}?
answer:1. Given the equation: [ frac{sin x}{1 + cos x} = frac{1}{3} ] We recognize that: [ frac{sin x}{1 + cos x} = tan frac{x}{2} ] Therefore: [ tan frac{x}{2} = frac{1}{3} ]2. We need to find: [ frac{sin 2x}{1 + cos 2x} ] Using the double-angle identities for sine and cosine: [ sin 2x = 2 sin x cos x ] [ cos 2x = cos^2 x - sin^2 x ] However, we can use a simpler approach by recognizing another identity: [ frac{sin 2x}{1 + cos 2x} = tan x ]3. We know that: [ tan x = frac{2 tan frac{x}{2}}{1 - tan^2 frac{x}{2}} ] Substituting (tan frac{x}{2} = frac{1}{3}): [ tan x = frac{2 cdot frac{1}{3}}{1 - left(frac{1}{3}right)^2} ] Simplify the expression: [ tan x = frac{frac{2}{3}}{1 - frac{1}{9}} = frac{frac{2}{3}}{frac{8}{9}} = frac{2}{3} cdot frac{9}{8} = frac{2 cdot 9}{3 cdot 8} = frac{18}{24} = frac{3}{4} ]4. Therefore: [ frac{sin 2x}{1 + cos 2x} = tan x = frac{3}{4} ]The final answer is (boxed{frac{3}{4}})
question:5. Let S denote the set of all positive integers whose prime factors are elements of {2,3,5,7,11}. (We include 1 in the set S.) Ifsum_{q in S} frac{varphi(q)}{q^{2}}can be written as frac{a}{b} for relatively prime positive integers a and b, find a+b. (Here varphi denotes Euler's totient function.)
answer:1. Understanding the Problem: We need to find the sum (sum_{q in S} frac{varphi(q)}{q^2}), where (S) is the set of all positive integers whose prime factors are elements of ({2, 3, 5, 7, 11}), and (varphi) is Euler's totient function. We need to express this sum as a fraction (frac{a}{b}) in simplest form and find (a + b).2. Using the Multiplicative Property: Since (frac{varphi(q)}{q^2}) is a multiplicative function, we can write: [ sum_{q in S} frac{varphi(q)}{q^2} = prod_{p in {2, 3, 5, 7, 11}} left( sum_{i=0}^{infty} frac{varphi(p^i)}{p^{2i}} right) ]3. Simplifying the Inner Sum: For a prime (p), (varphi(p^i) = p^i - p^{i-1}) for (i geq 1) and (varphi(1) = 1). Therefore: [ sum_{i=0}^{infty} frac{varphi(p^i)}{p^{2i}} = 1 + sum_{i=1}^{infty} frac{p^i - p^{i-1}}{p^{2i}} = 1 + sum_{i=1}^{infty} left( frac{1}{p^i} - frac{1}{p^{i+1}} right) ] This series is telescoping: [ 1 + left( frac{1}{p} - frac{1}{p^2} right) + left( frac{1}{p^2} - frac{1}{p^3} right) + cdots = 1 + frac{1}{p} ]4. Product Over All Primes in the Set: Therefore, we have: [ sum_{q in S} frac{varphi(q)}{q^2} = prod_{p in {2, 3, 5, 7, 11}} left( 1 + frac{1}{p} right) ] Calculating each term: [ 1 + frac{1}{2} = frac{3}{2}, quad 1 + frac{1}{3} = frac{4}{3}, quad 1 + frac{1}{5} = frac{6}{5}, quad 1 + frac{1}{7} = frac{8}{7}, quad 1 + frac{1}{11} = frac{12}{11} ]5. Multiplying the Fractions: [ prod_{p in {2, 3, 5, 7, 11}} left( 1 + frac{1}{p} right) = frac{3}{2} cdot frac{4}{3} cdot frac{6}{5} cdot frac{8}{7} cdot frac{12}{11} ] Simplifying the product: [ frac{3 cdot 4 cdot 6 cdot 8 cdot 12}{2 cdot 3 cdot 5 cdot 7 cdot 11} = frac{1152}{385} ]6. Finding (a + b): The fraction (frac{1152}{385}) is already in simplest form since 1152 and 385 are relatively prime. Thus, (a = 1152) and (b = 385). Therefore, (a + b = 1152 + 385 = 1537).The final answer is (boxed{1537}).
question:2. As shown in Figure 1, each face of the cube has a positive integer. It is known that the sum of the numbers on opposite faces is equal. If the numbers opposite to 13, 9, 3 are a, b, c respectively, then the value of a^{2}+b^{2}+c^{2}-a b-b c-c a is ( ).(A) 48(B) 76(C) 96(D) 152
answer:2. B.According to the problem, we have13+a=9+b=3+c text {. }Thus, a-b=-4, b-c=-6, c-a=10.Then a^{2}+b^{2}+c^{2}-a b-b c-c a=frac{1}{2}left[(a-b)^{2}+(b-c)^{2}+(c-a)^{2}right]=76 .
question:In the sequence {a_n}, let S_n denote the sum of the first n terms, and S_n = 1 + ka_n (k neq 0, k neq 1).(1) Find a_n;(2) When k=-1, find the value of {a_1}^2 + {a_2}^2 + cdots + {a_n}^2.
answer:(1) Since S_1 = a_1 = 1 + ka_1, we have a_1 = -frac{k^{n-1}}{(k-1)^{n}}. Thus,a_n = frac{1}{1-k} cdot left(frac{k}{k-1}right)^{n} = -frac{k^{n-1}}{(k-1)^{n}}.(2) In the sequence {a_n}, we have left{{a_n}^2right} is a geometric sequence with first term {left(frac{1}{1-k}right)}^2 and common ratio {left(frac{1}{k-1}right)}^2.When k=-1, the geometric sequence left{{a_n}^2right} has first term frac{1}{4} and common ratio frac{1}{4}. Therefore,{a_1}^2 + {a_2}^2 + cdots + {a_n}^2 = frac{frac{1}{4}left(1-frac{1}{4^{n}}right)}{1-frac{1}{4}} = boxed{frac{1}{3}left(1-frac{1}{4^{n}}right)}.
question:The range of values for m when the graph of the function y=3^{-|x-1|}-m intersects the x-axis is ____.
answer:Since the graph of the function y=3^{-|x-1|}-m intersects the x-axis, it means we are looking at the range of values for the function m=3^{-|x-1|}. Therefore, the range of m for m=3^{-|x-1|} is m in (0, 1]. Hence, the range of real numbers for m is: 0 < m leq 1. Therefore, the answer is: boxed{(0, 1]}.