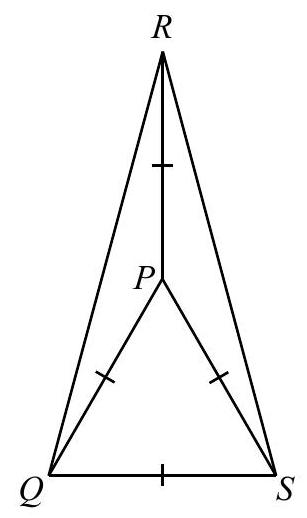
answer:Since triangle P Q S is equilateral, then angle Q P S=60^{circ}.Since angle R P Q, angle R P S and angle Q P S completely surround point P, then the sum of their measures is 360^{circ}.Since angle R P Q=angle R P S, this means that 2 angle R P Q+angle Q P S=360^{circ} or 2 angle R P Q=360^{circ}-60^{circ}, which means that angle R P Q=angle R P S=150^{circ}.Since P R=P Q, then in isosceles triangle P Q R, we haveangle P R Q=angle P Q R=frac{1}{2}left(180^{circ}-angle R P Qright)=frac{1}{2}left(180^{circ}-150^{circ}right)=15^{circ}Similarly, angle P R S=angle P S R=15^{circ}.This means that angle Q R S=angle P R Q+angle P R S=15^{circ}+15^{circ}=30^{circ}.

answer:12. B. From the problem, we have 192 midleft(a^{3}-1right).begin{array}{l}text { Also, } 192=3 times 2^{6}, text { and } a^{3}-1=(a-1)[a(a+1)+1] =(a-1) a(a+1)+(a-1) .end{array}Since a(a+1)+1 is odd, we have2^{6}left|left(a^{3}-1right) Leftrightarrow 2^{6}right|(a-1) text {. }Also, 3 mid(a-1) a(a+1), so3left|left(a^{3}-1right) Leftrightarrow 3right|(a-1) text {. }Therefore, 192 mid(a-1). Thus, a=192 k+1.Given 0<a<2009, then k=0,1, cdots, 10.Hence, the sum of all possible positive integers a that satisfy the condition is 11+192(1+2+cdots+10)=10571.

answer:Assume that f: mathbb{R}^{+} rightarrow mathbb{R}^{+} and the polynomial P with non-negative coefficients and P(0)=0 satisfy the conditions of the problem. For positive reals with x>y, we shall write Q(x, y) for the relation:f(f(x)+P(y))=f(x-y)+2 y1. Step 1. f(x) geq x. Assume that this is not true. Since P(0)=0 and P is with non-negative coefficients, P(x)+x is surjective on positive reals. If f(x) < x, then there exists a positive real y such that f(x) = x - y. By Q(x, y), we get:f(f(x)+P(y))=f(x-y)+2 ySince f(x) = x - y, we have f(x-y) = f(f(x)+P(y)) geq f(x) + P(y) geq f(x) + 2y. Therefore, f(x-y) geq f(x). We get f(y) geq f(2y) geq cdots geq f(ny) geq ny for all positive integers n, which is a contradiction.2. Step 2. If c neq 0, then f(f(x)+2z+c^2) = f(x+1) + 2(z-1) + 2c for z > 1. Indeed, by Q(f(x+z) + cz, c), we get:f(f(f(x+z) + cz) + c^2) = f(f(x+z) + cz - c) + 2c = f(x+1) + 2(z-1) + 2cOn the other hand, by Q(x+z, z), we have:f(x) + 2z + c^2 = f(f(x+z) + P(z)) + c^2 = f(f(x+z) + cz) + c^2Substituting in the LHS of Q(f(x+z) + cz, c), we get f(f(x) + 2z + c^2) = f(x+1) + 2(z-1) + 2c.3. Step 3. There is x_0 such that f(x) is linear on (x_0, infty). If c neq 0, then by Step 2, fixing x=1, we get f(f(1) + 2z + c^2) = f(2) + 2(z-1) + 2c which implies that f is linear for z > f(1) + 2 + c^2. As for the case c=0, consider y, z in (0, infty). Pick x > max(y, z), then by Q(x, x-y) and Q(x, x-z) we get:f(y) + 2(x-y) = f(f(x)) = f(z) + 2(x-z)which proves that f(y) - 2y = f(z) - 2z and therefore f is linear on (0, infty).4. Step 4. P(y) = y and f(x) = x on (x_0, infty). By Step 3, let f(x) = ax + b on (x_0, infty). Since f takes only positive values, a geq 0. If a=0, then by Q(x+y, y) for y > x_0 we get:2y + f(x) = f(f(x+y) + P(y)) = f(b + cy)Since the LHS is not constant, we conclude c neq 0, but then for y > x_0 / c, we get that the RHS equals b which is a contradiction.Hence a > 0. Now for x > x_0 and x > (x_0 - b) / a large enough by P(x+y, y) we get:ax + b + 2y = f(x) + 2y = f(f(x+y) + P(y)) = f(ax + ay + b + cy) = a(ax + ay + b + cy) + b.Comparing the coefficients before x, we see a^2 = a and since a neq 0, a = 1. Now 2b = b and thus b = 0. Finally, equalizing the coefficients before y, we conclude 2 = 1 + c and therefore c = 1.Now we know that f(x) = x on (x_0, infty) and P(y) = y. Let y > x_0. Then by Q(x+y, x) we conclude:f(x) + 2y = f(f(x+y) + P(y)) = f(x + y + y) = x + 2yTherefore f(x) = x for every x. Conversely, it is straightforward that f(x) = x and P(y) = y do indeed satisfy the conditions of the problem.

answer:Let AC=5 be the diagonal of the given quadrilateral ABCD, and O be the center of the inscribed circle in the quadrilateral. The center of the circle inscribed in an angle lies on the bisector of that angle, so triangles ABC and ADC are equal by side and two adjacent angles.Denote AB=AD=x, BC=CD=y, angle ABC=alpha. Thenx+y=7, frac{1}{2} x y sin alpha=6, x y=frac{12}{sin alpha}, x^2+y^2-2 x y cos alpha=25,x^2+y^2-2 x y cos alpha=(x+y)^2-2 x y-2 x y cos alpha=49-2 x y(1+cos alpha)=25, x y=frac{12}{1+cos alpha}From the equality frac{12}{1+cos alpha}=frac{12}{sin alpha}, it follows that 1+cos alpha=sin alpha. Squaring both sides of this equation and simplifying, we get the equation cos alpha(1+cos alpha)=0, and since 0<alpha<180^{circ}, then alpha=90^{circ}.Thusleft{begin{array}{l}x+y=7 x y=12end{array}right.From this system, we find that x=3, y=4 or x=4, y=3, and the area of triangle ABC is 6.Points A and C are equidistant from the endpoints of segment BD, so AC is the perpendicular bisector of segment BD. From the equality frac{1}{2} AC cdot BD=12 (the area of quadrilateral ABCD), we find thatBD=frac{2 cdot 12}{AC}=frac{2 cdot 12}{5}=frac{24}{5}## Answerfrac{24}{5}, 3,4,3,4.## Problem

answer:AnswerGiven log_a 2 = m and log_a 5 = n, we can rewrite a^{3m+n} using the properties of logarithms. First, recall that log_a b = c implies a^c = b. Therefore, from log_a 2 = m, we have a^m = 2, and from log_a 5 = n, we have a^n = 5.Now, consider a^{3m+n}. This can be rewritten as a^{3m} cdot a^n. Using the properties of exponents, this is equal to (a^m)^3 cdot a^n. Substituting the values we found earlier, this becomes 2^3 cdot 5 = 8 cdot 5 = 40.Therefore, the correct answer is boxed{text{D}}.

answer:Method 1: The scenarios of having at least 1 girl among the 4 people include 1 girl and 3 boys, and 2 girls and 2 boys. Therefore, the number of different selection schemes is C^1_2 times C^3_4 + C^2_2 times C^2_4 = 2 times 4 + 1 times 6 = 14.Method 2: Selecting 4 people from 4 boys and 2 girls in total has C^4_6 ways. The selection scheme that includes 4 boys has C^4_4 ways. Therefore, the number of schemes that include at least 1 girl is C^4_6 - C^4_4 = 15 - 1 = 14.Thus, the correct answer is boxed{text{A}}.Analysis: Method 1: By direct calculation, considering the scenarios of having at least 1 girl among the 4 people, which include 1 girl and 3 boys, and 2 girls and 2 boys, we calculate the number of selection schemes for each scenario. By the principle of addition, we can obtain the answer.Method 2: By the method of exclusion, we first calculate the number of selection schemes for choosing 4 people from 4 boys and 2 girls, then calculate the number of schemes that include 4 boys. By the method of exclusion, we can obtain the answer.