answer:17. Let the sum of all positive divisors of a positive integer a be b. Let d_{1}, d_{2}, cdots, d_{n} be the positive divisors of a arranged in ascending order, so d_{1}=1, d_{n}=a. Since the least common multiple of the denominators in S=sum_{i=1}^{n} frac{1}{d_{i}} is d_{n}=a, we haveS=sum_{i=1}^{n} frac{d_{n+1-i}}{d_{n}}=frac{1}{d_{n}} sum_{i=1}^{n} d_{i}=frac{b}{a} .Given a=360=2^{3} times 3^{2} times 5, we haveb=left(1+2+2^{2}+2^{3}right) timesleft(1+3+3^{2}right) times(1+5)=1170 text {. }Therefore, the sum of the reciprocals of all positive divisors of 360 is frac{1170}{360}=frac{13}{4}.

answer:From f(x-4)=-f(x), we can deduce that f(x-8)=f(x), hence the period of the function is 8.Since the function is odd, we can also deduce that f(x-4)=f(-x).Given that f(x) is monotonically increasing on the interval [0,2], it follows that f(x) is also monotonically increasing on the interval [-2,0].Since f(0)=0, the function is monotonically increasing on the interval [-2,2].Therefore, f(4)=-f(4-4)=-f(0)=0, f(3)=-f(3-4)=-f(-1)=f(1),Using the fact that the function is monotonically increasing on the interval [-2,2], we get f(-1) < f(0) < f(1),which means f(-1) < f(4) < f(3),Hence, the correct choice is: boxed{text{D}}.From the problem, we know that the period of the function is 8, f(x-4)=f(-x), f(0)=0, and the function is monotonically increasing on the interval [-2,2].Based on f(4)=-f(0)=0, f(3)=-f(3-4)=f(1), we can deduce f(-1) < f(0) < f(1), leading to the conclusion.This problem mainly examines the comprehensive application of the odd-even properties and monotonicity of functions, and is considered a medium-level question.

answer:According to the problem, let the line l intersect the circle at points A and B.The circle x^2+y^2-2y=0 can be rewritten as x^2+(y-1)^2=1, with center (0,1) and radius r=1.The distance d between the center of the circle and the line l is given by:d = frac{|1|}{sqrt{2}} = frac{sqrt{2}}{2}Then, the length of the chord AB is given by:AB = 2 times sqrt{1 - left(frac{1}{2}right)} = sqrt{2}Thus, the answer is: boxed{sqrt{2}}.To solve this problem, we first determine the intersection points of the line and the circle by setting their equations equal to each other. Then, we analyze the center and radius of the circle, calculate the distance between the center and the line, and finally use the distance formula to find the length of the chord. This problem involves the properties of lines and circles intersecting and the calculation of chord length, making it a basic-level question.

answer:Answer: A C=13.Solution. (Fig. 3). First, we prove that M I=M A (trident lemma).Indeed, the external angle A I M of triangle A I B is equal to the sum of angles B A I and A B I, and since A I and B I are angle bisectors, angle A I M=frac{1}{2} angle A+frac{1}{2} angle B. Angle I A M is equal to the sum of angles I A C and C A M. But angle I A C=frac{1}{2} angle A, and angle C A M=angle C B M=frac{1}{2} angle B as inscribed angles.From this, it follows that angle I A M=frac{1}{2} angle A+frac{1}{2} angle B=angle A I M, and therefore, triangle A M I is isosceles, M I=M A. By the condition M O= M I, so by the trident lemma A O=M O=M I=M A. This means that triangle A O M is equilateral and angle A O M=60^{circ}. Since the central angle A O M is twice the inscribed angle A B M, we have frac{1}{2} angle B=30^{circ}, that is, angle B=60^{circ}.By the cosine theorem, A C^{2}=A B^{2}+B C^{2}-2 cdot A B cdot B C cos 60^{circ}= 13^{2}.Criteria. Answer without explanation - 0 points. Proved that angle B is 60^{circ}-5 points. Points are not deducted for the absence of proof of the trident lemma. Full solution - 7 points.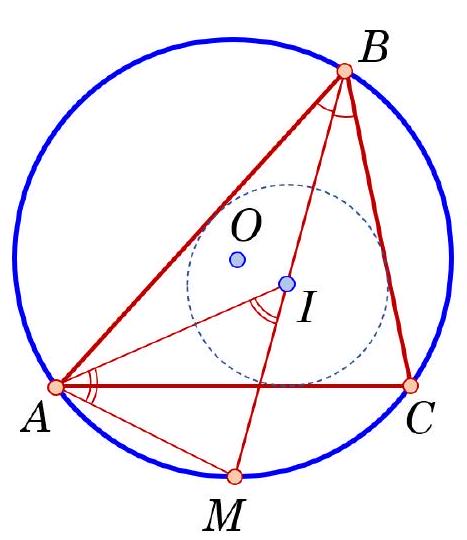Fig. 3

answer:6. 20 .First, consider S=frac{6}{7}+frac{6^{2}}{7}+cdots+frac{6^{2010}}{7}.In equation (1), no term is an integer, but the sum of any two adjacent terms is an integer (since frac{6^{k}}{7}+frac{6^{k+1}}{7}=6^{k} (k in mathbf{Z}) is an integer).If the sum of two non-integer numbers is an integer, then the sum of their integer parts is 1 less than the sum of the numbers themselves. Since there are 2010 terms in equation (1), the value of the desired sum P is 1005 less than S.Using the formula for the sum of a geometric series, we getbegin{array}{l}S=frac{6left(6^{2010}-1right)}{35} . text { Therefore, } 35 P=35(S-1005) =6^{2011}-6-35 times 1005 . text { Also, } 6^{2011}=6(35+1)^{1005} =6 times 35^{2} M+6 times 35 times 1005+6left(M in mathbf{N}_{+}right) Rightarrow 35 P=6 times 35^{2} M+5 times 35 times 1005 Rightarrow P=6 times 35 M+5 times 1005 .end{array}Therefore, the remainder when P is divided by 35 is equal to5 times 1005=5025divided by 35.Thus, the remainder when P is divided by 35 is 20.

answer:AnalysisThis problem involves solving an absolute value inequality, which is a basic type of problem.Step-by-Step Solution1. We start with the given inequality: |x-a| < b.2. By the definition of an absolute value inequality, we can rewrite this as a compound inequality: a-b < x < a+b.3. We are given that the solution set is { x | 2 < x < 4 }. This means that 2 < a-b and a+b < 4.4. We can rewrite these as a system of linear equations: begin{cases}a-b=2 a+b=4end{cases}5. Solving this system of equations, we find that a=3 and b=1.Final AnswerTherefore, the correct answer is boxed{C}.