answer:Solution: f'(x)=3ax^{2}+6x, (1) If a=0, then f(x)=3x^{2}+1geqslant 1, therefore f(x) has no zero points, which contradicts the condition; (2) If aneq 0, let f'(x)=0 to get x=0 or x=- dfrac {2}{a}. quad(1) If a > 0, then when x 0, f'(x) > 0, when - dfrac {2}{a} - dfrac {2}{a}, f'(x) 0, therefore f(x) is decreasing on (-infty,0), increasing on (0,- dfrac {2}{a}), and decreasing on (- dfrac {2}{a},+infty), therefore when x=0, f(x) reaches its minimum value 1, when x=- dfrac {2}{a}, f(x) reaches its maximum value, therefore f(x) has no zero points on (-infty,0) and has 1 zero point on (0,+infty), which meets the condition. therefore The range of values for a is boxed{(-infty,0)}.

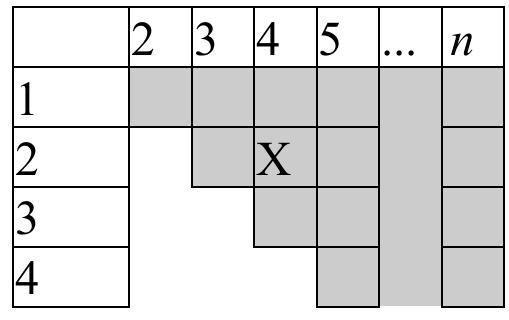
answer:Solution. It is convenient to form a triangular table. The shaded cells correspond to pairs of favorite socks. For example, the pair (2; 4), marked with an "X", corresponds to the case where the first favorite sock was the second one, and the second one was the fourth in the sequence. All pairs are equally likely, and their total number is C_{n}^{2}.The table shows the distribution of the random variable xi "Number of socks removed". Essentially, the table represents an inverted diagram of this distribution: the values of xi are taken from the first row, and the corresponding probabilities are depicted below them as shaded bars.xi simleft(begin{array}{cccccc}2 & 3 & cdots & k & cdots & n frac{1}{C_{n}^{2}} & frac{2}{C_{n}^{2}} & cdots & frac{k-1}{C_{n}^{2}} & & frac{n-1}{C_{n}^{2}}end{array}right)Let's find the expected value:begin{gathered}mathrm{E} xi=frac{1}{C_{n}^{2}} sum_{k=2}^{n} k(k-1)=frac{1}{C_{n}^{2}}left(sum_{k=2}^{n} k^{2}-sum_{k=2}^{n} kright)= =frac{1}{C_{n}^{2}}left(sum_{k=1}^{n} k^{2}-sum_{k=1}^{n} kright)=frac{1}{C_{n}^{2}}left(frac{n(n+1)(2 n+1)}{6}-frac{(n+1) n}{2}right)= =frac{1}{C_{n}^{2}} frac{n(n+1)(2 n-2)}{6}=frac{1}{C_{n}^{2}} frac{n(n+1)(n-1)}{3}=frac{2(n+1)}{3} .end{gathered}A geometric solution is possible: the expected value is the x-coordinate of the center of mass M of the diagram. Let's draw an auxiliary triangle with the same center of mass and find the x-coordinate. It is equal to the arithmetic mean of the x-coordinates of the vertices:frac{n+n+2}{3}=frac{2(n+1)}{3} text {. }| | 2 | 3 | 4 | 5 | ldots | n || :---: | :---: | :---: | :---: | :---: | :---: | :---: || 1 | | | | | | || 2 | | | | | | || 3 | | | | | | || 4 | | | | | | || 5 | | | | | | || n-1 | | | | | | vdots || | 2 | | | | frac{2(n+1)}{3} | n || | | | | | | |

answer:Solution: First notice that the sidelengths of triangle A B C are 3,4 and 5. By Pythagoras this implies that triangle A B C is right-angled at B. Now we can put the diagram on coordinate axes such that B=(0,0) and A=(0,3) and C=(4,0). Furthermore we get D=(0,2) and since E divides C A into the ratio 2: 3 we get E=(2.4,1.2), as shown in the diagram.Now we can calculate the slope of the line D E to be frac{-0.8}{2.4}=-frac{1}{3}. This means that the equation of line D E is given by y=-frac{x}{3}+2. Therefore the x-intercept of this line is the solution to 0=-frac{x}{3}+2. The solution is when x=6, and thus F=(6,0). Hence C F=2.

answer:Solution: (1) According to the problem, let A(x_{1},y_{1}) and B(x_{2},y_{2}), then we have y_{1}^{2}=8x_{1} and y_{2}^{2}=8x_{2}. Subtracting the two equations, we get (y_{1}-y_{2})(y_{1}+y_{2})=8(x_{1}-x_{2}). Since y_{1}+y_{2}=8, then k= dfrac {y_{2}-y_{1}}{x_{2}-x_{1}}=1, the slope of line AB is boxed{1}. (2) Given that F(2,0), the equation of line AB is y=x-2, substituting into y^{2}=8x to eliminate y and rearranging, we get x^{2}-12x+4=0, thus x_{1}+x_{2}=12, using the chord length formula, we find |AB|=(x_{1}+x_{2})+p=boxed{16}.

answer:Qaddama is 6 years older than Jack. Jack is 3 years younger than Doug. If Qaddama is 19 years old, how old is Doug?(A) 17(B) 16(C) 10(D) 18(E) 15## SolutionIf Qaddama is 6 years older than Jack and she is 19 years old, then Jack is 13 years old. If Jack is 3 years younger than Doug, then Doug must be 16 years of age.ANSwER: (B)

answer:Given that point A(a,4) lies on the hyperbola y=-frac{4}{x}, we can substitute the coordinates of point A into the equation of the hyperbola to find the value of a.Starting with the equation of the hyperbola y=-frac{4}{x} and substituting the y-coordinate of point A which is 4, we get:[4 = -frac{4}{a}]To solve for a, we can multiply both sides of the equation by a to get rid of the denominator on the right side, and then divide both sides by 4 to isolate a:[4a = -4 Rightarrow a = -frac{4}{4} Rightarrow a = -1]Therefore, the value of a that satisfies the condition given is -1. So, the correct answer is boxed{D}.