answer:Given the problem statement, we have the following equations:1. a = c - 2acos B2. c = 53. 3a = 2bFrom equation (3), we can express b in terms of a as b = frac{3}{2}a.Substituting c = 5 into the first equation and rearranging, we get:[a = 5 - 2acos B]By the Law of Cosines, we know that c^2 = a^2 + b^2 - 2abcos C. However, since we are dealing with side a and angle B, we rearrange the Law of Cosines to solve for a in terms of c, b, and cos B:[a = c - 2acos B = 5 - 2atimesfrac{a^2 + c^2 - b^2}{2ac}][= 5 - frac{a^2 + 25 - b^2}{5}][= frac{25 - a^2 - 25 + b^2}{5}][= frac{b^2 - a^2}{5}]Substituting b = frac{3}{2}a into the equation, we get:[a = frac{left(frac{3}{2}aright)^2 - a^2}{5}][= frac{frac{9}{4}a^2 - a^2}{5}][= frac{frac{5}{4}a^2}{5}][= frac{1}{4}a^2]To solve for a, we multiply both sides by 4:[4a = a^2]Rearranging the equation, we get:[a^2 - 4a = 0][a(a - 4) = 0]This gives us two possible solutions for a: a = 0 or a = 4. However, since a represents the length of a side in a triangle, a = 0 is not a valid solution. Therefore, we conclude that a = 4.Hence, the correct answer is boxed{A}.

answer:AnalysisThis question examines the method of calculating probability and is a basic question. When solving it, it is important to carefully read the question and make reasonable use of the enumeration method.First, calculate the number of basic events (a,b), which is n=4×4=16. Then, use the enumeration method to find the cases where the graph of the function y=a^{x}+b passes through the third quadrant. From this, the probability that the graph of the function y=a^{x}+b passes through the third quadrant can be calculated.SolutionSolution: Select a number from the set left{ frac{1}{2}, frac{1}{3}, 2, 3 right} and denote it as a. Select another number from the set {-2, -1, 1, 2} and denote it as b.The number of basic events (a,b) is n=4×4=16.Since the graph of the function y=a^{x}+b passes through the third quadrant in the following cases:1. When a=3, b=-1,2. When a=3, b=-2,3. When a=2, b=-1,4. When a=2, b=-2,5. When a= frac{1}{3}, b=-2,6. When a= frac{1}{2}, b=-2, there are a total of 6 cases,Therefore, the probability that the graph of the function y=a^{x}+b passes through the third quadrant is p= frac{6}{16}= frac{3}{8}.Hence, the answer is boxed{frac{3}{8}}.

answer:10. frac{1+sqrt{5}}{2}.Let the integer part of this positive number be n, and the decimal part be t. Then frac{n}{t}=frac{n+t}{n}=1+frac{t}{n}, so from 1<1+frac{t}{n}<2 we get 1<frac{n}{t}<2, thus 0<t<n<2 t<2 which gives n=1. Therefore, 1=t(t+1), solving the equation yields n+1:=frac{1+sqrt{5}}{2}.

answer:Let (A) be the geometric mean of the two numbers (sqrt {2}+1) and (sqrt {2}-1).Then, by the definition of the geometric mean, we have:begin{align*}A &= sqrt{(sqrt {2}+1) cdot (sqrt {2}-1)} &= sqrt{2 - 1} &= boxed{1}end{align*}Note that if two numbers have the same sign, they have two geometric means, which are equal in absolute value but opposite in sign. In this case, since both numbers are positive, they have only one positive geometric mean.

answer:(1) With Person A fixed at the head of the row, there are 6! = 720 different arrangements for the remaining people. So, there are boxed{720} different arrangements in total.(2) First, arrange Persons A, B, and C in 3! = 6 ways. Then, treat these three people as a single entity, making a total of 5 entities to be arranged (the trio as one plus the four other individuals). There are 5! = 120 ways to arrange these 5 entities. Therefore, the total number of arrangements where A, B, and C are together is 5! times 3! = 720. Thus, there are boxed{720} different arrangements in total.(3) First, arrange the four people who are not A, B, or C in 4! = 24 ways. These four create five potential "slots" where Persons A, B, and C can be placed (before the first person, between the first and second, and so on until after the fourth person). There are P(5,3) = frac{5!}{(5-3)!} = 60 ways to arrange A, B, and C in these slots. Thus, the total number of arrangements where A, B, and C are not next to each other is P(5,3) times 4! = 1440. Therefore, there are boxed{1440} different arrangements in total.(4) Without any restrictions, there would be 7! = 5040 different arrangements. If Person A is at the head, there are 6! = 720 arrangements no longer valid. Similarly, if Person B is in the middle, there are again 6! = 720 invalid arrangements. However, the configurations where A is at the head and B is in the middle have been counted twice, so we add back 5! = 120 valid arrangements. Therefore, the number of valid arrangements is 7! - 2 times 6! + 5! = 5040 - 1440 + 120 = 3720. So, there are boxed{3720} different arrangements in total.

answer:Solution.Let x be the distance between the first and second compressor stations, y the distance between the second and third, and z the distance between the first and third (Fig. 6).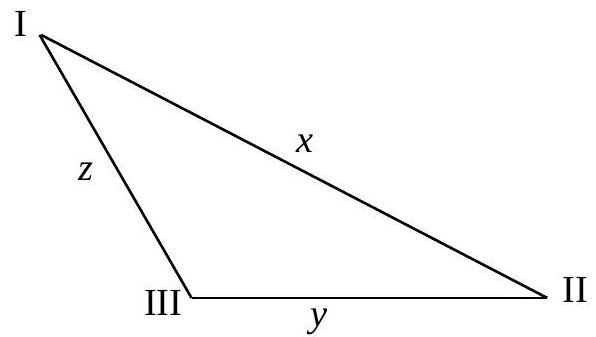Fig. 6According to the conditions of the problem, we form a system of equations:left{begin{array}{l}x+y=4 z z+y=x+a x+z=85end{array}right.From the third equation of the system, express z: z=85-x, we get the system left{begin{array}{l}x+y=4(85-x) 85-x+y=x+a ;end{array}right. left{begin{array}{l}5 x+y=340 2 x-y=85-a ;end{array}right. left{begin{array}{l}5 x+y=340, 7 x=425-a .end{array}right.Then, x=frac{425-a}{7}, y=frac{255+5 a}{7} z=frac{170+a}{7}.Determine all values of a for which the found values of x, y, and z would be possible. Using the triangle inequality (any side of a triangle is less than the sum of the other two sides), we form a system of inequalities to estimate the value of the parameter a:left{begin{array}{l}x<y+z y<x+z z<x+yend{array}right.left{begin{array}{l}frac{425-a}{7}<frac{255+5 a}{7}+frac{170+a}{7} frac{255+5 a}{7}<frac{425-a}{7}+frac{170+a}{7} frac{170+a}{7}<frac{425-a}{7}+frac{255+5 a}{7}end{array}right.Solving this system, we get that 0<a<68.Calculate the distances between the compressor stations when a=5: x=frac{425-5}{7}=60 km, y=frac{255+25}{7}=40 km, z=frac{170+5}{7}=25 km.Answer. 0<a<68 ; 60 km, 40 km, 25 km.