answer:Question 56, Solution: Organizing the knowledge:begin{array}{l}sin 4 x cdot sin 2 x - sin x cdot sin 3 x = -frac{1}{2}(cos 6 x - cos 2 x) - left[-frac{1}{2}(cos 4 x - cos 2 x)right] = frac{1}{2}(cos 4 x - cos 6 x)end{array}Let ( f(x) = frac{1}{2}(cos 4 x - cos 6 x) ), then ( f(pi - x) = frac{1}{2}[cos 4(pi - x) - cos 6(pi - x)] = frac{1}{2}(cos 4 x - cos 6 x) ). Therefore, ( f(x) ) is symmetric about the line ( x = frac{pi}{2} ). Hence, if ( sin 4 x cdot sin 2 x - sin x cdot sin 3 x = a ) has a solution in ( left(0, frac{pi}{2}right) ), it must also have a solution in ( left(frac{pi}{2}, piright) ), and thus it cannot have a unique solution. Therefore, the only possible unique solution is ( x = 0 ) or ( x = frac{pi}{2} ).If ( x = 0 ) is the unique solution, then ( a = 0 ). However, when ( a = 0 ), ( x = frac{pi}{5} ) is also a solution to ( sin 4 x cdot sin 2 x - sin x cdot sin 3 x = 0 ), which contradicts the assumption that ( x = 0 ) is the unique solution;If ( x = frac{pi}{2} ) is the unique solution, then ( a = sin 2 pi cdot sin pi - sin frac{pi}{2} cdot sin frac{3 pi}{2} = 1 ). Since ( sin 4 x cdot sin 2 x - sin x cdot sin 3 x = frac{1}{2}(cos 4 x - cos 6 x) leq 1 ), and in the interval ( [0, pi) ), only ( x = frac{pi}{2} ) can achieve 1, meaning that the only unique solution is ( x = frac{pi}{2} ).In summary, when ( a = 1 ), the equation has a unique solution.Note: The graph of ( f(x) = frac{1}{2}(cos 4 x - cos 6 x) ) is as follows:

answer:Given the area of triangle ABC is frac{{sqrt{3}({{b^2}+{c^2}-{a^2}})}}{4}, we start by recognizing a relationship between the sides of the triangle and its angles. The cosine rule tells us that b^{2}+c^{2}-a^{2}=2bccos A. This allows us to express the area in terms of the cosine of angle A:[frac{{sqrt{3}({{b^2}+{c^2}-{a^2}})}}{4} = frac{{sqrt{3}}}{2}bccos A]However, we also know that the area of a triangle can be expressed as frac{1}{2}bcsin A. Equating this to our given area expression, we have:[frac{1}{2}bcsin A = frac{{sqrt{3}}}{2}bccos A]Simplifying, we find that:[tan A = frac{sin A}{cos A} = sqrt{3}]Given that A is in the interval (0, pi), the angle whose tangent is sqrt{3} is frac{pi}{3}. Therefore, we conclude that:[A = boxed{frac{pi}{3}}]Hence, the correct answer is boxed{text{A}}.

answer:1.66. First, let's find the side AB = 2r (Fig. 1.52). Let ED = x. Then, using the equality AB + CD = BC + AD, we get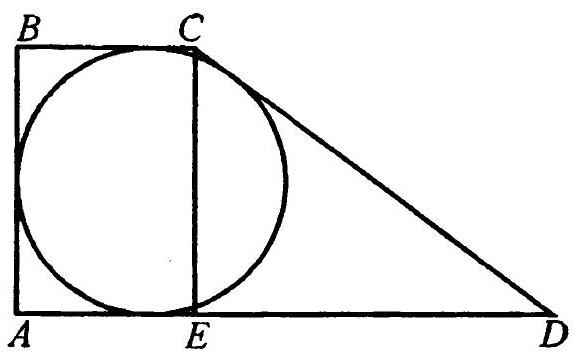Fig. 1.522r + CD = frac{4r}{3} + frac{4r}{3} + x, from which CD = frac{2r}{3} + x. In triangle CED, we have CD^2 = CE^2 + ED^2, or left(frac{2r}{3} + xright)^2 = 4r^2 + x^2, from which x = frac{8r}{3}. Therefore, CD = frac{10r}{3}, AD = frac{12r}{3} = 4r.Answer: 2r, frac{4r}{3}, frac{10r}{3}, and 4r.

answer:[Solution] Let birds alpha and beta be located at points A and B on circle C, respectively, and assume that birds alpha and beta can see each other. Let the number of birds that can be seen from point B but not from point A be k, and the number of birds that can be seen from point A but not from point B be h. Without loss of generality, assume k geqslant h. It is easy to see that if all the birds at point B are moved to point A, the number of visible pairs of birds will not increase. However, this reduces the number of points with birds by 1. Repeating this process until all visible birds are at the same point, the number of points with birds will be at most 35. If not, there would be at least 36 points with birds, and among these points, there must be two points with an arc length of no more than 10^{circ}, making the birds at these two points visible to each other, which is a contradiction. On the other hand, let A_{1}, A_{2}, cdots, A_{35} be the vertices of a regular 35-sided polygon inscribed in circle C. Then, the birds at A_{i} and A_{j} (i neq j) are not visible to each other. If the number of bird points n leqslant 34, then the n points can be moved to A_{1}, A_{2}, cdots, A_{n}. Since n leqslant 34, point A_{35} will have no birds. If A_{i} has at least two birds, then moving one bird from A_{i} to A_{35} will reduce the number of visible pairs. Continuing this process, we can ensure that there are exactly 35 points with birds, and these points are A_{1}, A_{2}, cdots, A_{35}.If there exist points A_{i} and A_{j} (i neq j) with bird counts x_{i} and x_{j}, respectively, and x_{i} geqslant x_{j} + 2, then moving one bird from A_{i} to A_{j} will reduce the number of visible pairs by at least 1. Continuing this process, we can ensure that the difference between any two of x_{1}, x_{2}, cdots, x_{35} does not exceed 1. It is clear that when 20 of these 35 numbers are 4 and 15 are 5, the number of visible bird pairs reaches its minimum value 20 binom{4}{2} + 15 binom{5}{2} = 270.

answer:1. The equation of the tangent line is boxed{x + y - 2 = 0}.2. When a leq 0, the function f(x) has no extreme values. When a > 0, the function f(x) has a minimum value at x = a, which is boxed{a - aln a}, and it has no maximum value.

answer:Since the line ax+4y+1=0 is parallel to the line 2x+y-2=0, their slopes must be equal. Therefore, -frac{a}{4} = -2, which gives a = 8. Hence, the answer is: 8. By equating their slopes, we get -frac{a}{4} = -2, and solve the equation for a. This problem examines the property of parallel lines, where parallel lines have equal slopes.Therefore, the final answer is boxed{8}.