Appearance
question:If 2x^{a}y^{3} and -x^{2}y^{b} are like terms, then a^{b} is equal to ( )A: 5B: 6C: 8D: 9
answer:To determine if 2x^{a}y^{3} and -x^{2}y^{b} are like terms, we need to compare the exponents of x and y in both terms. Like terms have the same variables raised to the same powers.1. Comparing the exponents of x, we get a = 2.2. Comparing the exponents of y, we get b = 3.Given these values, we can now calculate a^{b}:[a^{b} = 2^{3} = 8]Therefore, the correct answer is boxed{C}.
question:Determine the quadrant in which the point corresponding to the complex number z=(3+i)(1-i) is located in the complex plane.A: First quadrantB: Second quadrantC: Third quadrantD: Fourth quadrant
answer:To identify the quadrant where the point corresponding to the complex number z is located, we perform the multiplication of complex numbers (3+i) and (1-i). We need to remember the property that i^2 = -1. First, we distribute the terms: z = (3+i)(1-i) = 3 cdot 1 + 3 cdot (-i) + i cdot 1 - i cdot i Next, we simplify using the property i^2 = -1: z = 3 - 3i + i + 1 Combining like terms, we obtain: z = 4 - 2i In the complex plane, this corresponds to the point (4, -2). The x-coordinate is positive, and the y-coordinate is negative, which places the point in the fourth quadrant.So, the point corresponding to the complex number z in the complex plane is located in the fourth quadrant.Hence, the correct answer is boxed{text{D}}.
question:If the product of left(x+mright) and left(x+3right) does not contain a linear term of x, then m=______.
answer:To solve for m given that the product of left(x+mright) and left(x+3right) does not contain a linear term of x, we start by expanding the product:[begin{align*}left(x+mright)left(x+3right) &= x^2 + 3x + mx + 3m &= x^2 + (3+m)x + 3m.end{align*}]Given that the product does not contain a linear term of x, we set the coefficient of x to zero:[3+m = 0.]Solving this equation for m:[begin{align*}3 + m &= 0 m &= -3.end{align*}]Therefore, the value of m that satisfies the given condition is boxed{-3}.
question:2. Given the function f(x)=left(frac{1}{a^{x}-1}+frac{1}{2}right) cos x +b sin x+6 (where a and b are constants, and a>1), fleft(lg log _{8} 1000right)=8. Then the value of f(lg lg 2) is ( ).(A) 8(B) 4(C) -4(D) depends on the values of a and b
answer:2. (B).Let F(x)=f(x)-6.It is not hard to prove that F(-x)=-F(x), i.e., F(x) is an odd function.Thenbegin{array}{l}Fleft(-lg log _{8} 1000right)=-Fleft(operatorname{lglog}_{8} 1000right), F(operatorname{lglg} 2)=-F(operatorname{lglog} 8000), f(lg 22)-6=-left[fleft(operatorname{lglog}_{8} 1000right)-6right]end{array}Therefore, f(operatorname{lglg} 2)=-f(lg log 81000)+12=4.
question:Problem 1. a) Show that the numbera=sqrt{9-sqrt{77}} cdot sqrt{2} cdot(sqrt{11}-sqrt{7}) cdot(9+sqrt{77})is a natural number.b) Consider the real numbers x and y such that xy=6. If x>2 and y>2, show that x+y<5.Mathematical Gazette
answer:Problem 1. a) Show that the number a=sqrt{9-sqrt{77}} cdot sqrt{2} cdot(sqrt{11}-sqrt{7}) cdot(9+sqrt{77}) is a natural number.b) Consider the real numbers x and y such that x y=6. If x>2 and y>2, show that x+y<5.Gazeta Matematică## Solution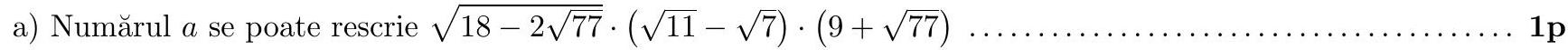As a result, a=(sqrt{11}-sqrt{7})^{2} cdot(9+sqrt{77})=(18-2 sqrt{77})(9+sqrt{77})=8 in mathbb{N} ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots .1 p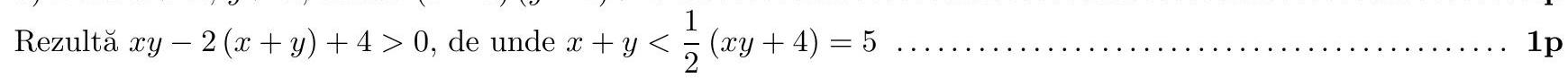
question:G6. A point O and the circles k_{1} with center O and radius 3, k_{2} with center O and radius 5, are given. Let A be a point on k_{1} and B be a point on k_{2}. If A B C is equilateral triangle, find the maximum value of the distance O C.
answer:## SolutionIt is easy to see that the points O and C must be in different semi-planes with respect to the line A B.Let O P B be an equilateral triangle ( P and C on the same side of O B ). Since angle P B C =60^{circ}-angle A B P and angle O B A=60^{circ}-angle A B P, then angle P B C=angle O B A. Hence the triangles A O B and C P B are equal and P C=O A. From the triangle O P C we haveO C leq O P+P C=O B+O A=8Hence, the maximum yalue of the distance O C is 8 (when the point P lies on O C )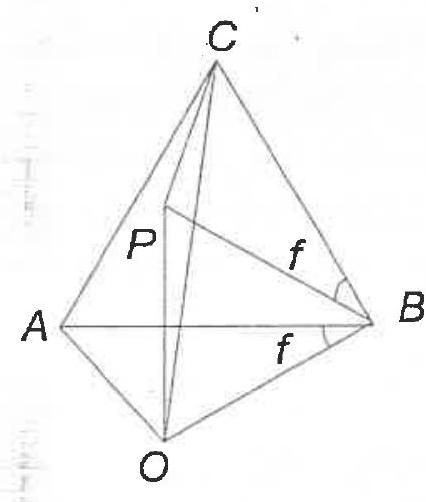Figure 8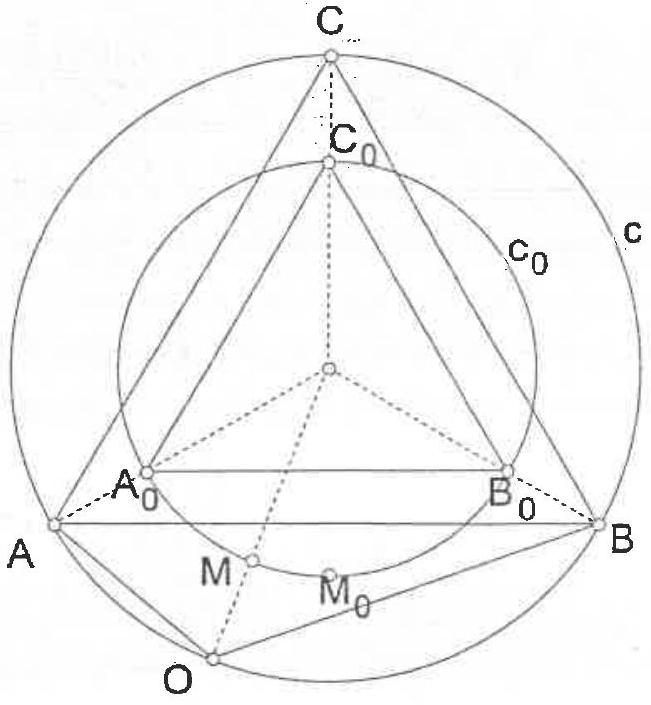Figure 9## Complement to the solutionIndeed there exists a triangle mathrm{OAB} with mathrm{OA}=3, mathrm{OB}=5 and mathrm{OC}=8.To construct such a triangle, let's first consider a point M on the minor arc widehat{A_{0} B_{0}} of the circumference left(c_{0}right) of an arbitrary equilateral triangle A_{0} B_{0} C_{0}. As mathrm{M} moves along widehat{mathrm{A}_{0} mathrm{~B}_{0}} from the midpoint position mathrm{M}_{0} towards mathrm{A}_{0}, the ratio frac{mathrm{MA}_{0}}{mathrm{MB}_{0}} takes on all the decreasing values from 1 to 0 . Thus there exists a position of mathrm{M} such that frac{mathrm{MA}_{0}}{mathrm{MB}_{0}}=frac{3}{5}. Now a homothesy centered at the center of left(mathrm{c}_{0}right) can take mathrm{A}_{0}, mathrm{~B}_{0}, mathrm{C}_{0}, mathrm{M} to the new positions mathrm{A}, mathrm{B}, mathrm{C}, mathrm{O} so that mathrm{OA}=3 and mathrm{OB}=5. Then, since mathrm{C} lies on the minor arc overparen{mathrm{AB}} of the circumference (c) of the equilateral triangle mathrm{ABC} we get mathrm{OC}=mathrm{OA}+mathrm{OB}=3+5=8 as wanted, (figure 9).