Appearance
question:1. Kolya went to the store in the neighboring village on an electric scooter at a speed of 10 km/h. Having traveled exactly one third of the entire distance, he realized that with the previous speed, he would arrive exactly when the store closes, and he doubled his speed. But when he had traveled exactly 2 / 3 of the entire distance, the scooter broke down, and Kolya walked the remaining part of the way. At what speed did he walk if he arrived exactly when the store closed?
answer:Answer: 6 frac{2}{3} km/h.Solution. Let the distance to the village be 3 x km. If Kolya had traveled the entire time at a speed of 10 mathrm{km} / h, he would have spent 3 x / 10 hours on the road. This is the time from his departure to the store's closing. The first third of the distance Kolya traveled in x / 10 hours. Doubling his speed, Kolya traveled the second third of the distance in x / 20 hours. Thus, for two-thirds of the distance, he spent x / 10 + x / 20 = 3 x / 20 hours. Therefore, 3 x / 10 - 3 x / 20 = 3 x / 20 hours remained until the store's closing, and during this time he managed to travel x km. Thus, he traveled at a speed of x: frac{3 x}{20} = frac{20}{3} km/h.
question:7.1. Masha and the Bear ate a basket of raspberries and 60 pies, starting and finishing at the same time. At first, Masha was eating raspberries, and the Bear was eating pies, then (at some point) they switched. The Bear ate raspberries 6 times faster than Masha, and pies only 3 times faster. How many pies did the Bear eat, if he ate twice as many raspberries as Masha?
answer:Answer: 54 pies. Solution: Divide the raspberries into 3 equal parts. The bear ate each part 6 times faster than Masha, but there are two parts, so he spent only 3 times less time on the raspberries than Masha. This means Masha ate pies in one-third of the time the bear did. Since she eats three times slower, she ate 9 times fewer pies than the bear. Dividing the pies in the ratio of 9:1, we see that Masha got the 10th part, which is 6 pies. The remaining 54 pies went to the bear.Criterion: Correct answer - no less than 2 points, with full justification - 7 points.
question:6. [4 points] Two parallel lines ell_{1} and ell_{2} touch the circle omega_{1} with center O_{1} at points A and B respectively. The circle omega_{2} with center O_{2} touches the line ell_{1} at point D, intersects the line ell_{2} at points B and E, and intersects the circle omega_{1} again at point C (with point O_{2} lying between the lines ell_{1} and ell_{2}). It is known that the ratio of the area of quadrilateral B O_{1} C O_{2} to the area of triangle O_{2} B E is frac{6}{5}. Find the ratio of the radii of the circles omega_{2} and omega_{1}.
answer:Answer: frac{R_{2}}{R_{1}}=frac{7}{6}.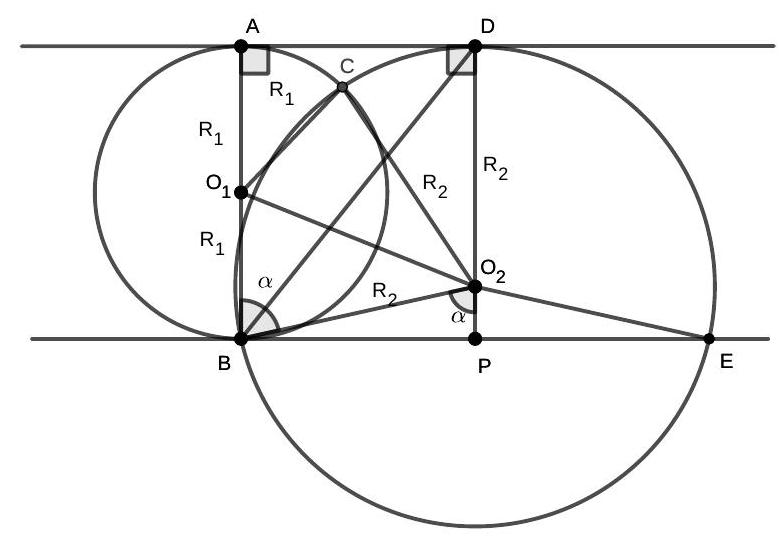Fig. 3: Option 10, Problem 6Solution. a) Let R_{1}, R_{2} be the radii of the circles omega_{1}, omega_{2} respectively, angle O_{1} B O_{2}=alpha, and the lines D O_{2} and ell_{2} intersect at point P. Then, from the condition of tangency, angle O_{2} B E=frac{pi}{2}-alpha, and angle B O_{2} P=frac{pi}{2}-angle O_{2} B E=alpha. Triangles B O_{1} O_{2} and C O_{1} O_{2} are equal by three sides, so S_{B O_{1} C O_{2}}=2 S_{O_{1} B O_{2}}=2 cdot frac{1}{2} cdot B O_{1} cdot B O_{2} cdot sin alpha=R_{1} R_{2} sin alpha. The area of triangle B O_{2} E is frac{1}{2} O_{2} P cdot B E=frac{1}{2} R_{2} cos alpha cdot 2 R_{2} sin alpha=R_{2}^{2} sin alpha cos alpha. Therefore, frac{6}{5}=frac{S_{B O_{1} O_{2}}}{S_{B O_{2} E}}=frac{R_{1}}{R_{2} cos alpha}, which means frac{5}{6} R_{1}=R_{2} cos alpha. Further, A B=D P, so 2 R_{1}=R_{2}+R_{2} cos alpha, hence 2 R_{1}=R_{2}+frac{5}{6} R_{1}, and frac{R_{2}}{R_{1}}=frac{7}{6}.
question:Factorize x^4-1 within the complex number range.
answer:Since x^4-1 can be written as:[x^4-1 = (x^2+1)(x^2-1)][= (x+i)(x-i)(x-1)(x+1).]Therefore, the answer is boxed{(x+i)(x-i)(x-1)(x+1)}.
question:A B C is a triangle from whose medians we construct another triangle; from the medians of this new triangle we construct yet another triangle, and so on to infinity. What is the sum of the areas of these triangles if the area of the original triangle is t?
answer:I. Solution. The midpoints of the sides of triangle ABC are A', B', C'. Extend C'B' to D so that B'D = B'C'.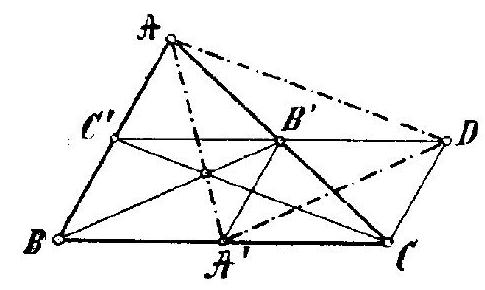Since B'D is equal and parallel to BA', it follows that A'D = BB'. But CD is equal and parallel to AC', so AD = CC'. Therefore, triangle ADA' is the triangle constructed from the medians of the original triangle. Let's calculate the area t' of this triangle:t' = triangle AA'B' + triangle AB'D + triangle DB'A'buttriangle AA'B' = triangle AB'C' = frac{1}{4} triangle ABC = frac{1}{4} tand similarly,triangle AB'D = frac{1}{4} t text{ and } triangle DB'A' = frac{1}{4} tthust' = frac{3}{4} tSimilarly, we find that the area of the triangle constructed from the medians of the triangle with area t' is t'' = frac{3}{4} t' = left(frac{3}{4}right)^2 t, and so on.Thus, the areas of the triangles form an infinite geometric series with the first term t and common ratio frac{3}{4}. Therefore, the sum of the series is:S = frac{t}{1 - frac{3}{4}} = 4t(Károly Szabó.)II. Solution.Let the medians of the triangle with area t be k_1, k_2, k_3 and k_1 + k_2 + k_3 = k; then (K.M.L.IV. year, p. 63)t = frac{4}{3} sqrt{k(k - k_1)(k - k_2)(k - k_3)}The area of the triangle constructed from the medians is:t' = sqrt{k(k - k_1)(k - k_2)(k - k_3)}and thust' = frac{3}{4} tThe problem was also solved by: Dénes A., Détshy K., Erdős A., Fekete J., Freibauer E., Goldziher K., Kertész L., Koós A., Kornis Ö., Krisztián Gy., Lukhaub Gy., Manheim I., Perl Gy., Raab L., Roth M., Sasvári G., Schiffer H., Szabó I., Weisz Á., Weisz J.
question:A set of three real numbers can be represented as left{ a, frac{b}{a}, 1 right} and also as {a^2, a+b, 0}. Find the value of a^{2019} + b^{2018} = ________.
answer:Step 1:Since the two sets are equal, we can write the system of equations:begin{cases} frac{b}{a} = 0 a^2 = 1 a^2 neq a + b end{cases}Step 2:From the first equation, we have b = 0.Step 3:Substitute b = 0 into the second equation: a^2 = 1. This gives us a = -1 or a = 1.Step 4:Substitute the values of a and b into the third equation: a^2 neq a + b. If a = 1, then 1 neq 1 + 0, which is false. Therefore, a = -1.Step 5:Now, compute a^{2019} + b^{2018} = (-1)^{2019} + (0)^{2018} = -1.Thus, the answer is boxed{-1}.