answer:There are two cases to consider. The first case is when line l is parallel to line MN. In this case, the equation of line l is 4x + y - 6 = 0. The second case is when line l passes through the midpoint of MN, which is (3, -1). In this case, the equation of line l is 3x + 2y - 7 = 0. Therefore, the equations of line l are either 4x + y - 6 = 0 or 3x + 2y - 7 = 0.Thus, the equation of line l is boxed{4x + y - 6 = 0 text{ or } 3x + 2y - 7 = 0}.

answer:389 div 4 = 97 remainder 1, 97 div 4 = 24 remainder 1, 24 div 4 = 6 remainder 0, 6 div 4 = 1 remainder 2, 1 div 4 = 0 remainder 1, Arrange the remainders from bottom to top: 12011. Thus, (389)_{10} = (12011)_{4}. The last digit is 1. Therefore, the answer is boxed{1}.

answer:Solution. We havemeasuredangle P Q N=measuredangle A Q B=180^{circ}-frac{alpha+beta}{2}=90^{circ}+frac{gamma}{2}Furthermore, from the cyclic quadrilateral P Q N C it follows that measuredangle P Q N=180^{circ}-gamma, so from these two relations we get gamma=60^{circ}. Now,measuredangle Q N P=measuredangle Q C P=frac{gamma}{2}=30^{circ}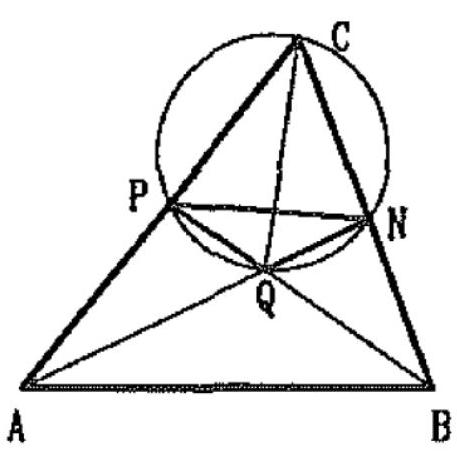and similarly measuredangle N P Q=30^{circ}, so triangle N P Q is isosceles, with base angles of 30^{circ}. By the perpendicular bisector Q C of the base N P, it can be divided into two congruent triangles that can form an equilateral triangle with height frac{1}{2} P N=frac{1}{2}, which means the side length is frac{sqrt{3}}{3}. Finally, its area is equal to frac{sqrt{3}}{12}.

answer:Answer: 8.Solution. We will express all distances in kilometers, time in hours, and speed in kilometers per hour. Let the distance between the village and the city be S, the speed of the truck be x, and the speed of the car be y. The time until the first meeting is frac{S}{x+y}, so the distance from the village to the actual meeting point is frac{S x}{x+y}.In the first hypothetical scenario, the truck will travel 0.75 x kilometers in 45 minutes, meaning it will take another frac{S-0.75 x}{x+y} hours to reach the expected first meeting point, and the truck will travel another frac{(S-0.75 x) x}{x+y} kilometers. According to the problem, we know that18=0.75 x+frac{(S-0.75 x) x}{x+y}-frac{S x}{x+y}=0.75 frac{x y}{x+y}from which we find frac{x y}{x+y}=18 cdot frac{4}{3}=24.In the second scenario, the car will travel y / 3 kilometers in 20 minutes, meaning it will take another frac{S-y / 3}{x+y} hours to reach the expected second meeting point, and the truck will travel frac{(S-y / 3) x}{x+y} kilometers during this time. The value we need to find isfrac{S x}{x+y}-frac{(S-y / 3) x}{x+y}=frac{x y / 3}{x+y}=24 / 3=8Another solution. Instead of the scenario "the truck left 45 minutes earlier," we will consider the scenario "the car left 45 minutes later" - it is clear that the meeting point will be the same in this case.We will solve the problem graphically. Along the O x axis, we will plot the coordinates of the vehicles such that the city corresponds to the coordinate 0 and the village to the coordinate p>0. Along the O t axis, we will plot time (the common start of movement in the original scenario will correspond to t=0). We will represent the car's movement with a red line and the truck's movement with a blue line; in addition, we will mark two alternative graphs of the car's movement (with a start 45 minutes later and 20 minutes earlier). The meeting point in the original scenario (location and time) will be denoted by A, and in the alternative scenarios by B and C: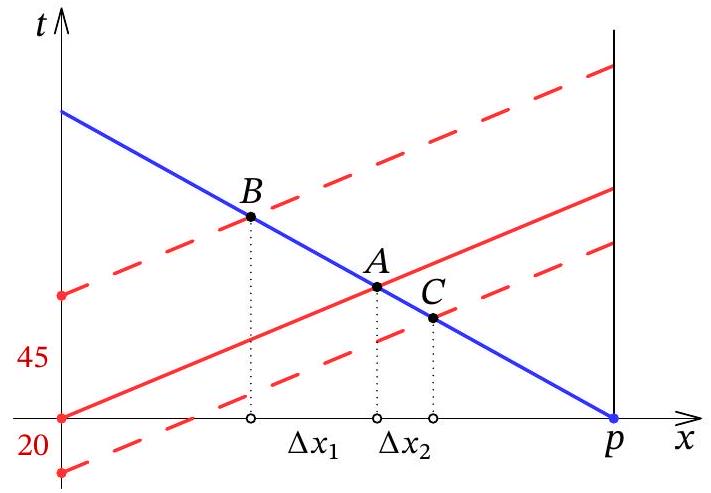By Thales' theorem,frac{45}{20}=frac{A B}{A C}=frac{Delta x_{1}}{Delta x_{2}}Since Delta x_{1}=18 kilometers according to the problem, then Delta x_{2}=8 kilometers.

answer:(The cross-section of a cube can be an acute triangle, isosceles triangle, equilateral triangle, but it cannot be an obtuse triangle or a right triangle; for quadrilaterals, it can be an isosceles trapezoid, parallelogram, rhombus, rectangle, but it cannot be a right trapezoid; for pentagons, it can be any pentagon, but it cannot be a regular pentagon; for hexagons, it can be a regular hexagon. Answer: (B).)

answer:Solution. The given equation is linear if we consider x as a function of y:frac{d x}{d y}-x cos y=sin 2 yWe apply the method of variation of arbitrary constants. First, we solve the corresponding homogeneous equationfrac{d x}{d y}-x cos y=0which is a separable variable equation. Its general solution isx=C e^{sin y}, quad C=text { const. }We seek the general solution of equation (4) in the formx=C(y) e^{sin y}where C(y) is an unknown function of y. Substituting (5) into (4), we getC^{prime}(y) e^{sin y}+C(y) e^{sin y} cos y-C(y) e^{sin y} cos y=sin 2 yorC^{prime}(y)=e^{-sin y} sin 2 yFrom this, integrating by parts, we havebegin{aligned}& C(y)=int e^{-sin y} sin 2 y d y=2 int e^{-sin y} cos y sin y d y= & =2 int sin y dleft(-e^{-sin y}right)=2left(-sin y e^{-sin y}+int e^{-sin y} cos y d yright)= & =2left(-sin y e^{-sin y}-e^{-sin y}right)+Cend{aligned}Thus,C(y)=-2 e^{-sin y}(1+sin y)+C .Substituting (6) into (5), we obtain the general solution of equation (4), and hence of the given equation:x=C e^{sin y}-2(1+sin y) . quad DeltaEquation (1) can also be integrated as follows. We assumey=u(x) v(x)where u(x) and v(x) are unknown functions of x, one of which, for example v(x), can be chosen arbitrarily. Substituting (7) into (1), after transformation we getv u^{prime}+left(p v+v^{prime}right) u=q(x) .Defining v(x) from the condition v^{prime}+p v=0, we then find from (8) the function u(x), and consequently, the solution y=u v of equation (1). As v(x), we can take any particular solution of the equation v^{prime}+p v=0, v not equiv.