answer:The line connecting the centers of two tangent circles passes through their point of tangency.## SolutionLet the radii of the given circles be r, r and R (r < R). Then the sides of the specified triangle are R - r, R - r, and 2r. Therefore,Consequently, R = 9.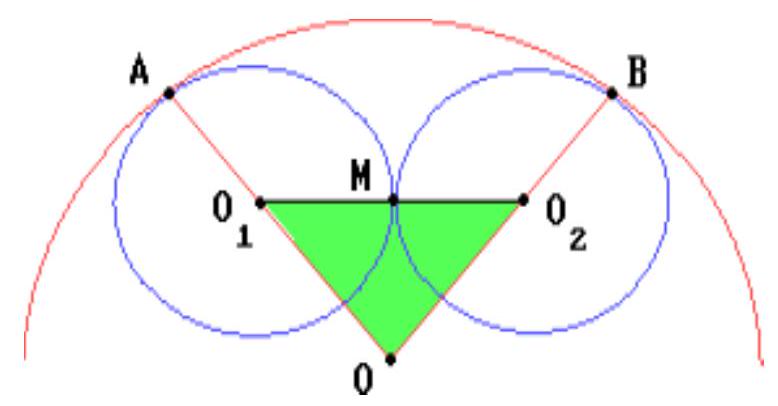Answer9.Send a comment

answer:In triangle A B C, from angle B A C=angle B C A=44^{circ}, we getA B=B C, angle A B C=92^{circ} text {. }As shown in Figure 6, draw B D perpA C at point D, extend C Mto intersect B D at point O, and connectO A. Then we havebegin{array}{l}angle O A C=angle M C A =30^{circ}, angle B A O=angle B A C-angle O A C=44^{circ}-30^{circ}=14^{circ}, angle O A M=angle O A C-angle M A C=30^{circ}-16^{circ}=14^{circ} .end{array}Therefore, angle B A O=angle M A O.text { Also, } angle A O D=90^{circ}-angle O A D=90^{circ}-30^{circ}=60^{circ}=angle C O D text {, }Therefore, angle A O M=120^{circ}=angle A O B.Since A O=A O, thus, triangle A B O cong triangle A M O.Hence O B=O M.Given angle B O M=120^{circ}, therefore,angle O M B=angle O B M=frac{180^{circ}-angle B O M}{2}=30^{circ} text {. }Therefore, angle B M C=180^{circ}-angle O M B=150^{circ}.

answer:Answer: 27.Solution. If the blue beads are arranged in a circle, the number of pairs of adjacent beads is equal to the number of beads. Since there is a red bead between any two blue beads, there are no fewer red beads in the necklace than blue ones. Similarly, it can be proven that there are no fewer green beads than red ones. Therefore, there are no fewer than frac{80}{3}=26 frac{2}{3} green beads, which means there are at least 27. An example of a necklace containing exactly 27 green beads is as follows:GKR 3 GKR ... ; GKR (26 times); GK.

answer:Analysis: The test point is the profit and loss problem.This type of question requires students to master the basic method of solving application problems by setting up equations or the problem-solving approach for profit and loss.In the distribution process, we find that the second distribution plan is short of 7, but there are several situations where it is short of 7. Which one is it? By observing the first distribution plan, we can find that the total number of peaches must be a multiple of 3. Since the second plan is to distribute 7 peaches to each monkey, the distributed quantity must also be a multiple of 3, so the missing part must also be a multiple of 3, which means it is short of 3 or 6.If it is short of 6, (27+6) div(7-5) cannot be divided evenly, which does not meet the requirement, so it is excluded;If it is short of 3, (27+3) div(7-5)=15 (monkeys), the total number of peaches is: 15 times 5+27=102 (peaches)

answer:To solve these problems, follow the step-by-step enhancements to the original solutions:(1) We start with the expression (2frac{1}{4})^{frac{1}{2}} - (pi - 1)^{0} - (3frac{3}{8})^{-frac{2}{3}}:1. Convert the mixed numbers to improper fractions: [ (2frac{1}{4})^{frac{1}{2}} = left(frac{9}{4}right)^{frac{1}{2}}, quad (3frac{3}{8})^{-frac{2}{3}} = left(frac{27}{8}right)^{-frac{2}{3}}. ] 2. Since any nonzero number raised to the power of 0 is 1, we have (pi - 1)^{0} = 1.3. Apply exponent rules to simplify: [ left(frac{9}{4}right)^{frac{1}{2}} = frac{3}{2}, quad left(frac{27}{8}right)^{-frac{2}{3}} = left(left(frac{3}{2}right)^{3}right)^{-frac{2}{3}} = left(frac{3}{2}right)^{-2} = frac{4}{9}. ] 4. Compute the final expression: [ frac{3}{2} - 1 - frac{4}{9} = frac{1}{2} - frac{4}{9} = frac{9}{18} - frac{8}{18} = frac{1}{18}. ]Hence, the value of expression (1) is boxed{frac{1}{18}}.(2) Moving on to the second expression log_{3}left(frac{sqrt{3}}{3}right) + lg 5 + lg 0.2 + 7^{log_{7}{2}}:1. Utilize logarithmic properties to simplify: [ log_{3}left(frac{sqrt{3}}{3}right) = log_{3}3^{-frac{1}{2}} = -frac{1}{2}. ] 2. Apply the logarithm property lg(ab) = lg a + lg b: [ lg 5 + lg 0.2 = lg (5 times 0.2) = lg 1 = 0. ] 3. The last term exploits a property of logarithms and exponentiation with the same base: [ 7^{log_{7}{2}} = 2. ]4. Add all the terms together: [ -frac{1}{2} + 0 + 2 = frac{3}{2}. ]Consequently, the value of expression (2) is boxed{frac{3}{2}}.

answer:I. solution. Express the K expression depending on three parameters in terms of a single parameter, for example, x. From the conditional equations, by adding and rearranging,y=frac{10}{7}-xand using this, for example, from (2),z=frac{9}{7}-frac{3}{2} xBased on the condition, x cannot be negative, but it can take the value 0, because when x=0, according to (4) and (5), y and z are positive, so the minimum value of x is 0. On the other hand, from the fact that y and z are non-negative, (4) and (5) implyx leq frac{10}{7}, quad text { and } quad x leq frac{6}{7}so the maximum value of x is frac{6}{7}.Using (4) and (5),K=5 x-6 y+7 z=frac{x}{2}+frac{3}{7}the value of this expression increases with x, so its minimum and maximum values, by substituting the minimum and maximum values of x,K_{min }=frac{3}{7}, quad text { and } quad K_{max }=frac{6}{7}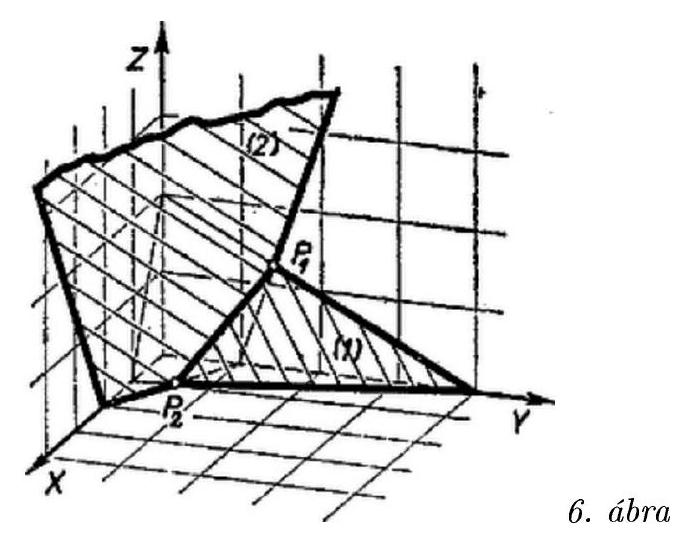II. solution. Visualize the three-variable expressions in the problem using a three-dimensional Cartesian coordinate system. (This solution assumes knowledge of certain elements of three-dimensional coordinate geometry.)The equations (2) and (3) each define a plane in space (Figure 6). The triples of numbers that satisfy both equations are the coordinates of points lying on the intersection line of these two planes. Due to the additional conditions x geq 0, y geq 0, z geq 0, only the part of this intersection line that lies in the first octant (and on its boundary) is relevant, which extends from the point P_{1}(0,10 / 7,9 / 7) to the point P_{2}(6 / 7,4 / 7,0).The equation 5 x-6 y+7 z=K defines a plane for each given value of K, which intersects the X, Y, and Z axes ata=K / 5, quad b=-K / 6, quad c=K / 7These intercepts are proportional to K, so the intersection lines of the planes corresponding to different K values with the coordinate planes are parallel, and thus the planes themselves are parallel.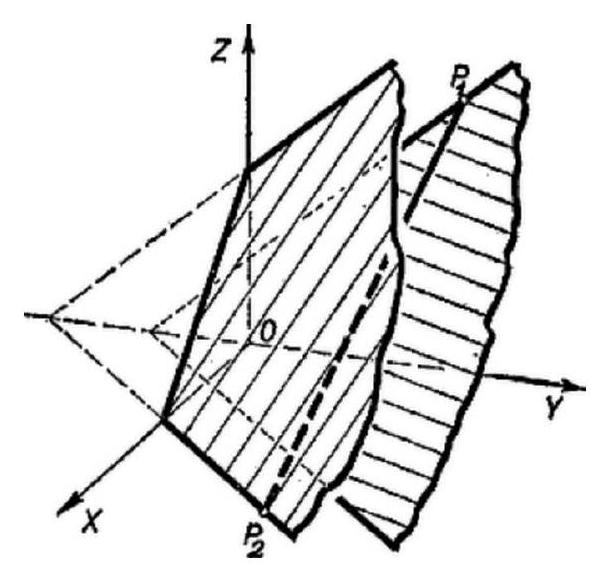Let's represent the plane of the parallel family passing through P_{1} and P_{2} (Figure 7). The value of K at P_{1} is 3 / 7, and at P_{2} it is 6 / 7, which are different, so different planes of the family pass through P_{1} and P_{2}. The intercepts arebegin{array}{llll}a_{1}=3 / 35, & b_{1}=-3 / 42, & c_{1}=3 / 49, & text { and } a_{2}=6 / 35, & b_{2}=-6 / 42, & c_{2}=6 / 49 &end{array}For each internal point of the segment P_{1} P_{2}, exactly one plane of the parallel family passes through it, lying between the two drawn planes. From the intercepts, it can be determined that K increases from P_{1} to P_{2}, so the above K_{1} is the minimum, and K_{2} is the maximum value.