answer:Triangles A B C and G A C are similar.## SolutionLet C G=t, angle C A G=alpha. Then B C=3 t, and since C E is the height, angle B=angle A C E. Since trapezoid A E F C is inscribed in a circle, it is isosceles, so angle A C E=alpha. Therefore, angle B=alpha. Consequently, right triangles A B C and G A C are similar by two angles. Thus,C G: A C=A C: B C, which means A C^{2}=C G cdot B C, or 12=3 t^{2}, from which t=2. operatorname{tg} alpha=C G / A C=frac{1}{sqrt{3}}, so alpha=30^{circ}.Therefore, A G=2 C G=4. By the tangent-secant theorem, G F=C G^{2} / G A=1.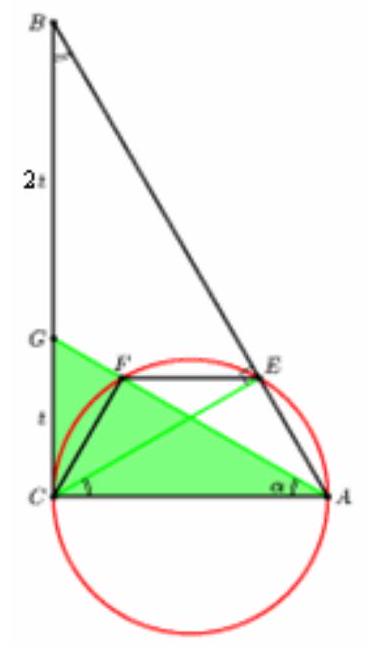## Answer1.

answer:2. 4 Detailed Explanation: Since a>b>0, then b(a-b) leqslantleft[frac{b+(a-b)}{2}right]^{2}=frac{a^{2}}{4}, so a^{2}+frac{1}{b(a-b)} geqslant a^{2}+frac{4}{a^{2}} geqslant 4, equality holds if and only if a=sqrt{2}, b=frac{sqrt{2}}{2}.

answer:Since chi^2=4.073, and P(chi^2geq3.841)approx0.05, P(chi^2geq5.024)approx0.025; Therefore, we can be boxed{95%} confident that there is a relationship between the two variables. Analysis: This conclusion is reached by looking up the values in a table.

answer:1. Define the problem and variables: - Brick of type A: dimensions (2 times 5 times 8) - Brick of type B: dimensions (2 times 3 times 7) - Box: dimensions (10 times 11 times 14)2. Calculate volumes: - Volume of the box: [ 10 times 11 times 14 = 1540 text{ unit cubes} ] - Volume of brick A: [ 2 times 5 times 8 = 80 text{ unit cubes} ] - Volume of brick B: [ 2 times 3 times 7 = 42 text{ unit cubes} ]3. Set up the equation for the total volume: [ 80x + 42y = 1540 ] where (x) is the number of type A bricks and (y) is the number of type B bricks.4. Simplify the equation: [ 80x + 42y = 1540 implies 40x + 21y = 770 ]5. Solve for (y) in terms of (x): [ 21y = 770 - 40x implies y = frac{770 - 40x}{21} ] For (y) to be an integer, (770 - 40x) must be divisible by 21.6. Find the general solution: [ 770 - 40x equiv 0 pmod{21} ] Simplify (770 pmod{21}): [ 770 div 21 = 36 text{ remainder } 14 implies 770 equiv 14 pmod{21} ] Thus: [ 14 - 40x equiv 0 pmod{21} implies -40x equiv -14 pmod{21} implies 40x equiv 14 pmod{21} ] Simplify (40 pmod{21}): [ 40 equiv 19 pmod{21} implies 19x equiv 14 pmod{21} ]7. Solve the congruence (19x equiv 14 pmod{21}): Find the multiplicative inverse of 19 modulo 21. Using the Extended Euclidean Algorithm: [ 19 cdot 10 equiv 1 pmod{21} implies x equiv 14 cdot 10 pmod{21} implies x equiv 140 pmod{21} implies x equiv 14 pmod{21} ] Thus: [ x = 14 + 21k quad text{for integer } k ]8. Substitute (x) back to find (y): [ y = frac{770 - 40(14 + 21k)}{21} = frac{770 - 560 - 840k}{21} = frac{210 - 840k}{21} = 10 - 40k ]9. Ensure non-negative solutions: [ x geq 0 implies 14 + 21k geq 0 implies k geq -frac{14}{21} implies k geq -1 ] [ y geq 0 implies 10 - 40k geq 0 implies k leq frac{10}{40} implies k leq frac{1}{4} ] Since (k) must be an integer, the only possible value is (k = 0).10. Substitute (k = 0): [ x = 14 + 21 cdot 0 = 14 ] [ y = 10 - 40 cdot 0 = 10 ]11. Verify the solution: [ 80 cdot 14 + 42 cdot 10 = 1120 + 420 = 1540 ] The solution is valid.12. Check the configuration: - The box can be filled with 14 bricks of type A and 10 bricks of type B as described in the solution.The final answer is (boxed{24})

answer:1. Given the function ( f(z) = (a + bi)z ), where ( a ) and ( b ) are positive numbers, and the property that the image of each point in the complex plane is equidistant from that point and the origin, we have: [ |f(z)| = |z - f(z)| ] This implies: [ |(a + bi)z| = |z - (a + bi)z| ]2. Simplify the right-hand side: [ |(a + bi)z| = |z(1 - (a + bi))| ] Since ( |kz| = |k||z| ) for any complex number ( k ): [ |a + bi||z| = |1 - (a + bi)||z| ] Dividing both sides by ( |z| ) (assuming ( z neq 0 )): [ |a + bi| = |1 - (a + bi)| ]3. Let ( a + bi = c ). Then: [ |c| = |1 - c| ] Given ( |c| = 8 ): [ 8 = |1 - c| ]4. Let ( c = a + bi ). Then: [ |1 - (a + bi)| = 8 ] This can be written as: [ |(1 - a) - bi| = 8 ]5. The magnitude of a complex number ( x + yi ) is given by ( sqrt{x^2 + y^2} ): [ sqrt{(1 - a)^2 + b^2} = 8 ]6. Squaring both sides: [ (1 - a)^2 + b^2 = 64 ]7. We also know that: [ a^2 + b^2 = 64 ]8. We now have two equations: [ (1 - a)^2 + b^2 = 64 ] [ a^2 + b^2 = 64 ]9. Subtract the second equation from the first: [ (1 - a)^2 + b^2 - (a^2 + b^2) = 64 - 64 ] [ (1 - a)^2 - a^2 = 0 ] [ 1 - 2a + a^2 - a^2 = 0 ] [ 1 - 2a = 0 ] [ a = frac{1}{2} ]10. Substitute ( a = frac{1}{2} ) into ( a^2 + b^2 = 64 ): [ left(frac{1}{2}right)^2 + b^2 = 64 ] [ frac{1}{4} + b^2 = 64 ] [ b^2 = 64 - frac{1}{4} ] [ b^2 = frac{256}{4} - frac{1}{4} ] [ b^2 = frac{255}{4} ]11. Given ( b^2 = frac{m}{n} ) where ( m ) and ( n ) are relatively prime positive integers, we have ( m = 255 ) and ( n = 4 ). Therefore: [ m + n = 255 + 4 = 259 ]The final answer is (boxed{259})

answer:After shifting the function y=sin 2x to the right by frac{pi}{12} units, we get the function y=sin 2(x-frac{pi}{12}).Then, stretching the abscissa of each point on the function graph to twice its original length (the ordinate remains unchanged), we obtain the function y=sin (x-frac{pi}{6}).Therefore, the answer is: boxed{y=sin (x-frac{pi}{6})}.This conclusion is drawn using the transformation rules of the function y=Asin (omega x+varphi).This question primarily tests the understanding of the transformation rules of the function y=Asin (omega x+varphi), and is considered a basic question.