answer:. The statement implies that if we translate the set of these disks by 0.02, the new set of disks is disjoint from the first. We can notably translate this set by two vectors overrightarrow{A B} and overrightarrow{A C} forming an angle of 60^{circ}: the first set of disks will be disjoint from the second and the third. But the second and the third will also be disjoint from each other, as we can go from one to the other by a third translation of 0.02 of vector overrightarrow{B C}, with A B C being an equilateral triangle. The three sets of disks thus obtained are not all within the initial square, but in a slightly larger square, with a side of 1.02. Since these sets are pairwise disjoint, the sum of their areas (which is three times each of the areas) is less than or equal to the area of the large square, which is 1.02^2 < 1.05. It follows that the area of the union of the initial disks is strictly less than frac{1.05}{3}=0.35.

answer:First, find the allowed values of x.left{begin{array} { l } { x neq 0 , } { 1 + frac { 1 } { x } neq 0 , } { 1 + frac { 1 } { 1 + frac { 1 } { x } } neq 0 }end{array} Rightarrow left{begin{array}{l}x neq 0, x neq-1, x neq-frac{1}{2} .end{array}right.right.From the left =frac{3 x+2}{2 x+1}, from the original equation we know frac{3 x+2}{2 x+1} geqslant 0.Solving this, we get x leqslant-frac{2}{3} or x>-frac{1}{2}.Combining (1) and (2), the solution to the original equation isx leqslant-frac{2}{3} and x neq-1 or x>-frac{1}{2} and x neq 0.

answer:1. We start with the given conditions: - ( f(i, i+1) = frac{1}{3} ) for all ( i ). - ( f(i, j) = f(i, k) + f(k, j) - 2f(i, k)f(k, j) ) for all ( k ) such that ( i < k < j ).2. We need to find ( f(1, 100) ). Using the second condition with ( i = 1 ), ( k = 2 ), and ( j = 100 ), we get: [ f(1, 100) = f(1, 2) + f(2, 100) - 2f(1, 2)f(2, 100) ] Given ( f(1, 2) = frac{1}{3} ), we substitute: [ f(1, 100) = frac{1}{3} + f(2, 100) - 2 cdot frac{1}{3} cdot f(2, 100) ] Simplifying, we get: [ f(1, 100) = frac{1}{3} + f(2, 100) - frac{2}{3}f(2, 100) ] [ f(1, 100) = frac{1}{3} + left(1 - frac{2}{3}right)f(2, 100) ] [ f(1, 100) = frac{1}{3} + frac{1}{3}f(2, 100) ] [ f(1, 100) = frac{1}{3}(1 + f(2, 100)) ]3. Similarly, we can express ( f(2, 100) ) using the same recurrence relation: [ f(2, 100) = f(2, 3) + f(3, 100) - 2f(2, 3)f(3, 100) ] Given ( f(2, 3) = frac{1}{3} ), we substitute: [ f(2, 100) = frac{1}{3} + f(3, 100) - 2 cdot frac{1}{3} cdot f(3, 100) ] Simplifying, we get: [ f(2, 100) = frac{1}{3} + f(3, 100) - frac{2}{3}f(3, 100) ] [ f(2, 100) = frac{1}{3} + left(1 - frac{2}{3}right)f(3, 100) ] [ f(2, 100) = frac{1}{3} + frac{1}{3}f(3, 100) ] [ f(2, 100) = frac{1}{3}(1 + f(3, 100)) ]4. By induction, we can generalize this pattern: [ f(1, n) = frac{1}{3}(1 + f(2, n)) ] [ f(2, n) = frac{1}{3}(1 + f(3, n)) ] [ vdots ] [ f(n-1, n) = frac{1}{3} ]5. We observe that: [ f(1, n) = frac{1}{3} left(1 + frac{1}{3} left(1 + frac{1}{3} left(1 + cdots left(1 + frac{1}{3}right) cdots right) right) right) ]6. This forms a geometric series: [ S_n = 1 + frac{1}{3} + frac{1}{3^2} + cdots + frac{1}{3^{n-1}} ] The sum of this geometric series is: [ S_n = frac{1 - left(frac{1}{3}right)^n}{1 - frac{1}{3}} = frac{1 - frac{1}{3^n}}{frac{2}{3}} = frac{3}{2} left(1 - frac{1}{3^n}right) ]7. Therefore: [ f(1, n) = frac{1}{3} S_n = frac{1}{3} cdot frac{3}{2} left(1 - frac{1}{3^n}right) = frac{1}{2} left(1 - frac{1}{3^n}right) ]8. For ( n = 100 ): [ f(1, 100) = frac{1}{2} left(1 - frac{1}{3^{100}}right) ]The final answer is (boxed{frac{1}{2} left(1 - frac{1}{3^{100}}right)})

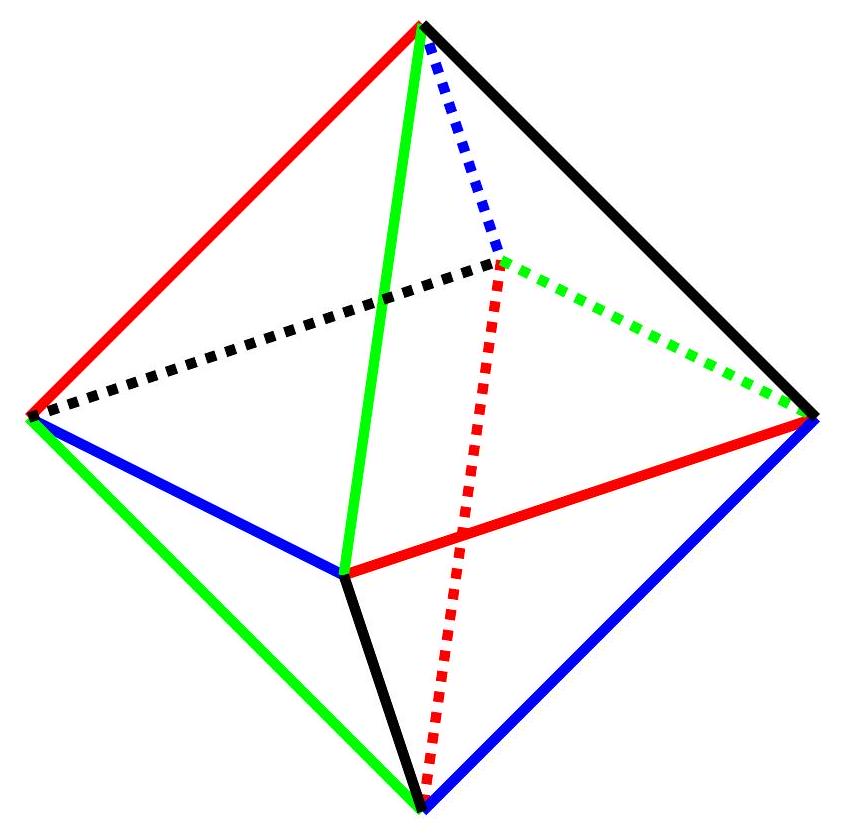
answer:Solution: Consider one of the colors. According to the condition, an edge of this color leaves each vertex. The total number of such exits is at least 6, and each edge leaves exactly two vertices. Therefore, the total number of edges of each color is at least 3. From this, it also follows that the number of edges of each color is no more than 6, otherwise there would not be enough edges of other colors.As can be seen from the diagram, the edges can be colored such that exactly one edge of each color leaves each vertex. The total number of colored edges will be 9, leaving 3 more edges. These 3 edges can be colored in any way. Depending on this, the number of green edges will vary from 3 to 6.Criteria: Only the answer - 0 points.Proved that the number of edges is at least 3 - 2 points.Proved that the number of edges is no more than 6 - 1 point.Example for each number of edges - 1 point each.These points are cumulative.

answer:Since in triangle ABC, it satisfies |overrightarrow{BC}| = |overrightarrow{AC}| and (overrightarrow{AB} - 3overrightarrow{AC}) perp overrightarrow{CB}, then (overrightarrow{AB} - 3overrightarrow{AC}) cdot overrightarrow{CB} = 0, Since overrightarrow{AB} = overrightarrow{AC} + overrightarrow{CB}, then |overrightarrow{CB}|^2 = 2overrightarrow{AC} cdot overrightarrow{CB}, thus |overrightarrow{CB}| cdot |overrightarrow{AC}| = -2overrightarrow{CA} cdot overrightarrow{CB}, therefore cos C = frac{overrightarrow{CA} cdot overrightarrow{CB}}{|overrightarrow{CB}| cdot |overrightarrow{CA}|} = -frac{1}{2}, Since C in (0, pi), therefore C = frac{2pi}{3}. Hence, the correct answer is: boxed{text{C}}. From the given information, (overrightarrow{AB} - 3overrightarrow{AC}) cdot overrightarrow{CB} = 0, thus |overrightarrow{CB}| cdot |overrightarrow{AC}| = -2overrightarrow{CA} cdot overrightarrow{CB}, and then cos C = frac{overrightarrow{CA} cdot overrightarrow{CB}}{|overrightarrow{CB}| cdot |overrightarrow{CA}|} = -frac{1}{2}, from which the size of angle C can be determined. This question examines the method of determining the size of an angle, which is a basic problem. When solving, it is important to apply the knowledge of vector operations appropriately.

answer:Given that the average of the data a, b, c is 5, we start by expressing this mathematically:[frac{1}{3}(a + b + c) = 5]From this equation, we want to find the average of the data a-2, b-2, c-2. We can express this new average as:[frac{1}{3}left((a-2) + (b-2) + (c-2)right) = frac{1}{3}(a + b + c - 6)]Since we know frac{1}{3}(a + b + c) = 5, we can substitute this value into our new equation:[frac{1}{3}(a + b + c - 6) = 5 - 2 = 3]Therefore, the average of the data a-2, b-2, c-2 is boxed{3}.