Appearance
question:Which of the following pairs of numbers has a greatest common factor of 20 ?(A) 200 and 2000(D) 20 and 25(B) 40 and 50(C) 20 and 40
answer:The greatest common factor of two numbers is the largest positive integer which divides into both numbers with no remainder.For answer (B), 50 divided by 20 leaves a remainder, so we may eliminate (B) as a possible answer.Similarly for answer (D), 25 divided by 20 leaves a remainder, so we may eliminate (D) as a possible answer.For answer (A), since 200 divides 200 and 200 divides 2000, the greatest common factor of 200 and 2000 cannot be 20 .For answer (E), since 40 divides 40 and 40 divides 80, the greatest common factor of 40 and 80 cannot be 20 .The largest positive integer which divides both 20 and 40 is 20 , and so (C) is the correct answer.
question:13.009. In the library, there are books in English, French, and German. English books make up 36 % of all foreign language books, French books make up 75 % of the English books, and the remaining 185 books are German. How many foreign language books are there in the library?
answer:## Solution.Let x be the total number of books in foreign languages. The number of English books is 0.36x; the number of French books is 0.75 cdot 0.36x. According to the problem, 0.36x + 0.75 cdot 0.36x + 185 = x, from which we find x = 500.Answer: 500
question:Given that f'(x) is the derivative of the function f(x), and f(1)=e, for any real number x, it holds that 2f(x)-f'(x) > 0. Then, the solution set of the inequality frac{f(x)}{e^{x}} < e^{x-1} is ______.
answer:Analysis Let g(x)=frac{f(x)}{e^{2x}}, and by studying its monotonicity on mathbb{R} using derivatives, we can solve the inequality. This problem tests the method of constructing functions to study the monotonicity of functions using derivatives, examining reasoning and computational skills, and is considered difficult. Solution Let g(x)=frac{f(x)}{e^{2x}}, then g'(x)=frac{e^{2x}f'(x)-2e^{2x}f(x)}{e^{4x}}= frac{f'(x)-2f(x)}{e^{2x}} 1, therefore the solution set of the inequality frac{f(x)}{e^{x}} < e^{x-1} is (1,+infty). Hence, the answer is boxed{(1,+infty)}.
question:5. In the non-decreasing sequence of positive odd numbers {1,3,3,3,5,5,5, 5,5, cdots}, each positive odd number k appears k times. It is known that there exist integers b, c, and d, such that for all integers n, a_{n}= b[sqrt{n+c}]+d, where [x] denotes the greatest integer not exceeding x. Then b+c+d equals
answer:5.2.Divide the known sequence into groups as follows:begin{array}{l}(1),(3,3,3),(5,5,5,5,5), cdots, (underbrace{2 k-1,2 k-1, cdots, 2 k-1}_{2 k-1 uparrow}),end{array}Let a_{n} be in the k-th group, where a_{n}=2 k-1. Then we havebegin{array}{l}1+3+5+cdots+2 k-3+1 leqslant n0, solving this gives sqrt{n-1}<k leqslant sqrt{n-1}+1.Therefore, k=[sqrt{n-1}+1]=[sqrt{n-1}]+1.Thus, a_{n}=2[sqrt{n-1}]+1.Hence, b+c+d=2+(-1)+1=2.
question:## Task A-4.2.We say that a semicircle is properly placed within a larger semicircle if their diameters are parallel, the endpoints of the diameter of the smaller semicircle lie on the semicircle of the larger semicircle, and the semicircle of the smaller semicircle touches the diameter of the larger semicircle.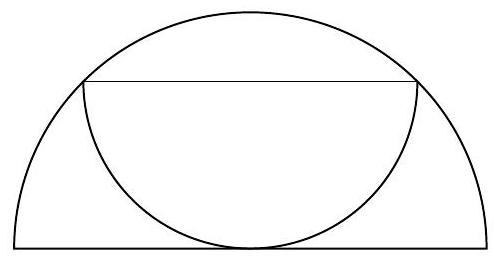A sequence of semicircles K_{1}, K_{2}, K_{3}, ldots is given, such that for each n in mathbb{N}, the semicircle K_{n+1} is properly placed within the semicircle K_{n}. The region that belongs to the semicircle K_{n} and does not belong to the semicircle K_{n+1} is colored blue if n is odd, and yellow if n is even.The radius of the semicircle K_{1} is 1. Determine the total area colored blue.
answer:## First Solution.Let the radius of the semicircle K_{n} be r_{n} and its area be P_{n} for n in mathbb{N}.Let overline{A B} be the diameter of the semicircle K_{1}, overline{C D} be the diameter of the semicircle K_{2}, and let F be the midpoint of the segment overline{C D}. Let the point E be the point of tangency between the semicircle K_{2} and the line A B.Then overline{E F} is the radius of the semicircle K_{2}, and it is perpendicular to the tangent A B. Since A B and C D are parallel, it follows that the lines C D and E F are also perpendicular.Since F is the midpoint of the segment overline{C D}, the line E F is the perpendicular bisector of that segment. The midpoint of the segment overline{A B} is the center of the semicircle on which the points C and D lie, and it also lies on the line E F. We conclude that F is precisely the midpoint of the segment overline{A B}.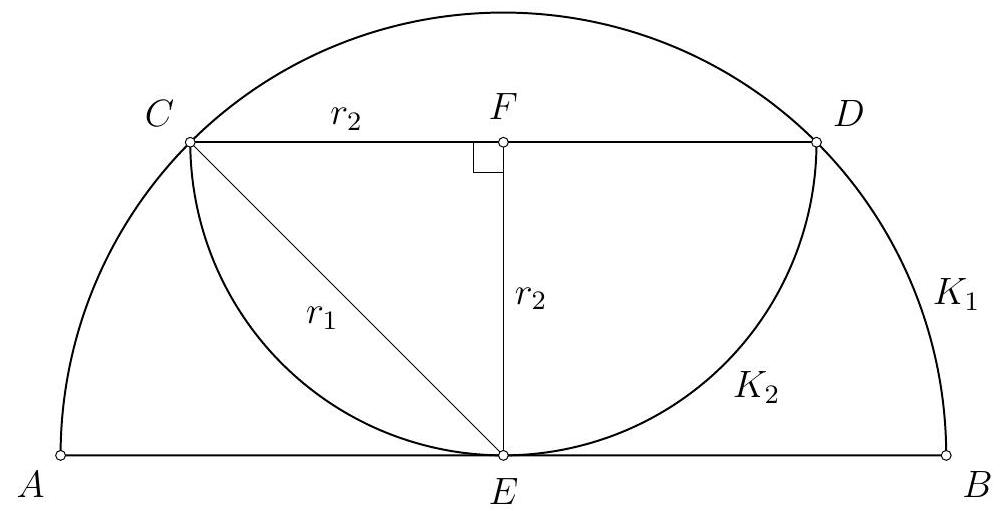As shown, triangle EFC is an isosceles right triangle with a right angle at vertex F. Its legs are of length |F E| = |F C| = r_{2} and the hypotenuse is of length |E C| = r_{1}. From the Pythagorean theorem for this triangle, we conclude that r_{2} = frac{1}{sqrt{2}} r_{1}.Similarly, r_{n+1} = frac{1}{sqrt{2}} r_{n}, orr_{n} = left(frac{1}{sqrt{2}}right)^{n-1}, quad text{for every } n in mathbb{N}Next, we calculate thatP_{n} = frac{1}{2} cdot r_{n}^{2} cdot pi = frac{1}{2} cdot left(frac{1}{2}right)^{n-1} cdot pi = frac{pi}{2^{n}}, quad text{for every } n in mathbb{N}The area covered by the blue color can be calculated by first adding the area of the blue P_{1}, then subtracting the area of the yellow P_{2}, then adding the area of the blue P_{3}, then subtracting the area of the yellow P_{4}, and so on. Thus, we seekP = P_{1} - P_{2} + P_{3} - P_{4} + cdotsSubstituting the expressions for P_{n}, we getbegin{aligned}P & = frac{pi}{2} - frac{pi}{4} + frac{pi}{8} - frac{pi}{16} + cdots & = frac{pi}{2} left(1 - frac{1}{2} + frac{1}{4} - frac{1}{8} + cdotsright) & = frac{pi}{2} cdot frac{1}{1 + frac{1}{2}} = frac{pi}{2} cdot frac{2}{3} = frac{pi}{3}end{aligned}In the second-to-last step, we used the formula for the sum of a geometric series:sum_{n=0}^{+infty} q^{n} = frac{1}{1 - q}, quad text{for } q = -frac{1}{2} in (-1, 1)
question:The point M lies inside the rhombus ABCD. It is known that angle DAB=110^o, angle AMD=80^o, angle BMC= 100^o. What can the angle angle AMB be equal?
answer:1. Identify the given angles and properties of the rhombus: - angle DAB = 110^circ - angle AMD = 80^circ - angle BMC = 100^circ - In a rhombus, opposite angles are equal, and adjacent angles are supplementary.2. Determine the angles of the rhombus: - Since angle DAB = 110^circ, the opposite angle angle BCD = 110^circ. - The adjacent angles angle ABC and angle ADC are supplementary to angle DAB and angle BCD, respectively. Therefore, angle ABC = angle ADC = 70^circ.3. Analyze the position of point M inside the rhombus: - Point M lies inside the rhombus, and we are given angle AMD = 80^circ and angle BMC = 100^circ.4. Use the properties of cyclic quadrilaterals: - Since angle AMD = 80^circ and angle BMC = 100^circ, we can infer that M lies on the circumcircles of triangles triangle AMD and triangle BMC.5. Determine the possible values of angle AMB: - The sum of the angles around point M should be 360^circ. Therefore, we have: [ angle AMD + angle BMC + angle AMB + angle CMD = 360^circ ] - Given angle AMD = 80^circ and angle BMC = 100^circ, we can write: [ 80^circ + 100^circ + angle AMB + angle CMD = 360^circ ] - Simplifying, we get: [ 180^circ + angle AMB + angle CMD = 360^circ ] [ angle AMB + angle CMD = 180^circ ]6. Determine the possible values of angle AMB: - Since angle CMD is an internal angle of the rhombus, it can be either 80^circ or 100^circ (depending on the position of M). - If angle CMD = 80^circ, then: [ angle AMB = 180^circ - 80^circ = 100^circ ] - If angle CMD = 100^circ, then: [ angle AMB = 180^circ - 100^circ = 80^circ ]Therefore, the possible values of angle AMB are 100^circ and 80^circ.The final answer is boxed{100^circ text{ or } 80^circ}